BasicPoicareMap class is mainly used for non-rigorous computations of Poincare Map. More...

#include <capd/poincare/BasicPoincareMap.h>

Public Types
typedef SolverT	Solver
	ODE solver type. More...

typedef Solver::VectorFieldType	VectorFieldType
	vector field type More...

typedef Solver::MatrixType	MatrixType
	matrix type More...

typedef Solver::VectorType	VectorType
	vector type More...

typedef Solver::ScalarType	ScalarType
	scalar entries type More...

typedef VectorType::size_type	size_type
	integral type used to index containers (vectors, matrices, etc) More...

typedef TypeTraits< ScalarType >::Real	RealType
	floating point type: for floating points is equal to ScalarType, for intervals is a type of their bounds. More...

typedef Solver::SolutionCurve	CurveType

typedef capd::diffAlgebra::SolutionCurve< CurveType >	SolutionCurve

typedef CurveType::HessianType	HessianType
	data structure for storing Hessians More...

typedef CurveType::JetType	JetType
	data structure for storing Hessians More...

typedef SectionT	SectionType
	Section function type. More...

typedef capd::poincare::CrossingDirection	CrossingDirection
	specifies direction of crossing of Poincare section (plus to minus, minus to plus or both) More...

Public Member Functions
	BasicPoincareMap (Solver &solver, SectionType &section, CrossingDirection direction=Both, const RealType &errorTolerance=pow(TypeTraits< RealType >::epsilon(), RealType(14.)/RealType(15.)))
	Constructor. More...

VectorType	operator() (const VectorType &v)
	Computes value of Poincare Map. More...

VectorType	operator() (VectorType v, ScalarType &in_out_time)
	Computes value of Poincare Map. More...

VectorType	operator() (const VectorType &v, VectorType &afterSection)
	Computes value of Poincare Map. More...

VectorType	operator() (VectorType v, VectorType &afterSection, ScalarType &in_out_time)
	Computes value of Poincare Map. More...

VectorType	operator() (const VectorType &v, MatrixType &dF)
	Computes value of Poincare Map and derivativeof the flow. More...

VectorType	operator() (VectorType v, MatrixType &dF, ScalarType &in_out_time)
	Computes value of Poincare Map and derivative of the flow. More...

VectorType	operator() (const VectorType &v, MatrixType &dF, HessianType &h)
	Computes value of Poincare Map, derivative and hessian of the flow. More...

VectorType	operator() (VectorType v, MatrixType &dF, HessianType &h, ScalarType &in_out_time)
	Computes value of Poincare Map, derivative and hessian of the flow. More...

VectorType	operator() (JetType &x)
	Computes Poincare Map and derivatives of the flow to given order evaluated at return time. More...

VectorType	operator() (JetType &x, ScalarType &in_out_time)
	Computes Poincare Map and derivatives of the flow to given order evaluated at return time. More...

MatrixType	computeDP (const VectorType &Px, const MatrixType &derivativeOfFlow, VectorType &dT, ScalarType returnTime=TypeTraits< ScalarType >::zero())
	Simultaneous computation of gradient of return time and derivative of Poincare Map dP. More...

MatrixType	computeDP (const VectorType &Px, const MatrixType &derivativeOfFlow, ScalarType returnTime=TypeTraits< ScalarType >::zero())
	Computes derivative of Poincare Map dP. More...

void	computeDP (const VectorType &Px, const MatrixType &derivativeOfFlow, const HessianType &hessianOfFlow, MatrixType &DP, HessianType &D2P, VectorType &dT, MatrixType &d2T, ScalarType returnTime=TypeTraits< ScalarType >::zero())
	Simultaneous computation of first and second Taylor coefficients of return time and Poincare map. More...

void	computeDP (const VectorType &Px, const MatrixType &derivativeOfFlow, const HessianType &hessianOfFlow, MatrixType &DP, HessianType &D2P, ScalarType returnTime=TypeTraits< ScalarType >::zero())
	Simultaneous computation of first and second Taylor coefficients of return time and Poincare map. More...

template<class JetT >
JetT	computeDP (const JetT &DPhi)
	Recomputes Taylor expansion of the flow into Taylor expansion of Poincare map. More...

const Solver &	getSolver () const
	Returns read-only reference to solver used to integrate the system. More...

Solver &	getSolver ()
	Returns reference to solver used to integrate the system. More...

const Solver &	getDynamicalSystem () const
	Returns read-only reference to solver used to integrate the system. More...

Solver &	getDynamicalSystem ()
	Returns reference to solver used to integrate the system. More...

VectorFieldType &	getVectorField ()
	Returns reference to solver used to integrate the system. More...

const VectorFieldType &	getVectorField () const
	Returns read-only reference to solver used to integrate the system. More...

const SectionType &	getSection () const
	Returns reference to Poincare section object. More...

size_type	getOrder () const
	Returns order of numerical method used. More...

ScalarType	getStep () const
	Returns time step. More...

void	setOrder (size_type newOrder)
	Sets order of Taylor method. More...

void	setSection (const SectionType &newSection)
	Sets new section function. More...

void	setStep (const ScalarType &newStep)
	Sets time step for integration of DS. More...

void	setFactor (double newFactor)

void	setCrossingDirection (CrossingDirection cs)

void	turnOnStepControl ()
	Disables automatic step control. More...

void	turnOffStepControl ()
	Enables automatic step control. Step control strategy is built in the solver. More...

void	onOffStepControl (bool sc)
	Disables or enables automatic step control. More...

void	setMaxReturnTime (double maxReturnTime)
	Sets maximal return time to Poincare section. If the trajectory does not reach the section during time [0,maxReturnTime] then an exception is thrown. This prevents looping of the procedure computing Poincare map in the case when the trajectory is captured by an attractor (like sink or attracting periodic orbit) and never intersect Poincare section. More...

void	setBlowUpMaxNorm (double blowUpMaxNorm)
	Sets threshold value of norm that is considered as a blow up of the solution. A trajectory may escape to infinity in finite time without crossing Poincare section. If the norm of a point on trajectory is bigger than this threshold value then an exception is thrown. More...

Protected Member Functions
template<typename T >
T	integrateUntilSectionCrossing (T &x, int n=1, ScalarType *lastStep=0)
	Given an initial condition the function computes its trajetory until -th intersection with the Poincare section. The point just before -th intersection is returned. More...

ScalarType	findRelativeCrossingTime (ScalarType timeJustBeforeSection, const CurveType &curve)
	This function computes time needed to cross the section from a point which is just before the section. Given solves for satisfying $\alpha(\varphi(t,x))=0$ by a Newton like scheme. This is just scalar equation with one unknown. Then, computed return time is used to integrate the point and compute Poincare map. More...

Protected Attributes
Solver &	m_solver
	dynamical system (e.g. Taylor, C2Taylor, CnTaylor, FadTaylor, etc) More...

const SectionType *	m_section
	section function More...

CrossingDirection	m_crossingDirection
	requested direction of section crossing More...

RealType	m_sectionFactor
	sectionFactor is used in the procedures reachSection and crossSection. IN NONRIGOROUS : we want to be closer than m_sectionFactor after section crossing IN RIGOROUS VERSION: Before and after section crossing we want the set to be closer to section than sectionFactor * sizeOfSet More...

double	m_blowUpMaxNorm

double	m_maxReturnTime

Detailed Description

template<typename SolverT, typename SectionT = AbstractSection<typename SolverT::MatrixType>>
class capd::poincare::BasicPoincareMap< SolverT, SectionT >

BasicPoicareMap class is mainly used for non-rigorous computations of Poincare Map.

For given Dynamical System and section it computes first return map and its derivatives but non-rigorously (i.e. without handling any computational errors).

Let $\varphi(t, x): R \times R^n -> R^n$ be a dynamical system Let $s: R^n \to R$ be a section function, Let $S = \{x \in R^n : s(x) = 0\}$ Let $P: S \to S$ be a Poincare Map For given point $x \in S$ let T(x) be first return time (in given crossing direction) i.e. $P(x) = \varphi(T(x), x) \in S$

In the following we denote by

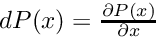
dP the derivative of Poincare Map P : $dP(x) = \frac{\partial P(x)}{\partial x}$
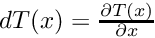
dT the derivative of T(x) : $dT(x) = \frac{\partial T(x)}{\partial x}$
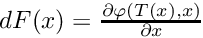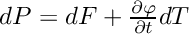
dF the derivative of the flow : $dF(x) = \frac{\partial \varphi(T(x), x)}{\partial x}$ Then $dP = dF + \frac{\partial \varphi}{\partial t} dT$

Parameters:

SolverT ODE solver
- SolverT::MapType vector field type
FunT - section function type
- FunT should have method gradient()

Member Typedef Documentation

◆ CrossingDirection

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

typedef capd::poincare::CrossingDirection capd::poincare::BasicPoincareMap< SolverT, SectionT >::CrossingDirection

specifies direction of crossing of Poincare section (plus to minus, minus to plus or both)

◆ CurveType

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

typedef Solver::SolutionCurve capd::poincare::BasicPoincareMap< SolverT, SectionT >::CurveType

◆ HessianType

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

typedef CurveType::HessianType capd::poincare::BasicPoincareMap< SolverT, SectionT >::HessianType

data structure for storing Hessians

◆ JetType

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

typedef CurveType::JetType capd::poincare::BasicPoincareMap< SolverT, SectionT >::JetType

data structure for storing Hessians

◆ MatrixType

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

typedef Solver::MatrixType capd::poincare::BasicPoincareMap< SolverT, SectionT >::MatrixType

matrix type

◆ RealType

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

typedef TypeTraits<ScalarType>::Real capd::poincare::BasicPoincareMap< SolverT, SectionT >::RealType

floating point type: for floating points is equal to ScalarType, for intervals is a type of their bounds.

◆ ScalarType

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

typedef Solver::ScalarType capd::poincare::BasicPoincareMap< SolverT, SectionT >::ScalarType

scalar entries type

◆ SectionType

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

typedef SectionT capd::poincare::BasicPoincareMap< SolverT, SectionT >::SectionType

Section function type.

◆ size_type

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

typedef VectorType::size_type capd::poincare::BasicPoincareMap< SolverT, SectionT >::size_type

integral type used to index containers (vectors, matrices, etc)

◆ SolutionCurve

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

typedef capd::diffAlgebra::SolutionCurve<CurveType> capd::poincare::BasicPoincareMap< SolverT, SectionT >::SolutionCurve

◆ Solver

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

typedef SolverT capd::poincare::BasicPoincareMap< SolverT, SectionT >::Solver

ODE solver type.

◆ VectorFieldType

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

typedef Solver::VectorFieldType capd::poincare::BasicPoincareMap< SolverT, SectionT >::VectorFieldType

vector field type

◆ VectorType

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

typedef Solver::VectorType capd::poincare::BasicPoincareMap< SolverT, SectionT >::VectorType

vector type

Member Function Documentation

◆ operator()()

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

VectorType capd::poincare::BasicPoincareMap< SolverT, SectionT >::operator()	(	const VectorType &	v,
		VectorType &	afterSection
	)

Computes value of Poincare Map.

Parameters

[in]	v	- argument of Poincare map
[out]	afterSection	- on output it contains a point just after first intersection with Poincare section that might be used for further integration.

Returns: P(v) - first intersection of the trajectory of v with Poincare section.

◆ setCrossingDirection()

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

void capd::poincare::BasicPoincareMap< SolverT, SectionT >::setCrossingDirection ( CrossingDirection cs )

inline

Member Data Documentation

◆ m_blowUpMaxNorm

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

double capd::poincare::BasicPoincareMap< SolverT, SectionT >::m_blowUpMaxNorm

protected

◆ m_crossingDirection

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

CrossingDirection capd::poincare::BasicPoincareMap< SolverT, SectionT >::m_crossingDirection

protected

requested direction of section crossing

◆ m_maxReturnTime

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

double capd::poincare::BasicPoincareMap< SolverT, SectionT >::m_maxReturnTime

protected

◆ m_section

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

const SectionType* capd::poincare::BasicPoincareMap< SolverT, SectionT >::m_section

protected

section function

◆ m_sectionFactor

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

RealType capd::poincare::BasicPoincareMap< SolverT, SectionT >::m_sectionFactor

protected

sectionFactor is used in the procedures reachSection and crossSection. IN NONRIGOROUS : we want to be closer than m_sectionFactor after section crossing IN RIGOROUS VERSION: Before and after section crossing we want the set to be closer to section than sectionFactor * sizeOfSet

◆ m_solver

template<typename SolverT , typename SectionT = AbstractSection<typename SolverT::MatrixType>>

Solver& capd::poincare::BasicPoincareMap< SolverT, SectionT >::m_solver

protected

dynamical system (e.g. Taylor, C2Taylor, CnTaylor, FadTaylor, etc)

The documentation for this class was generated from the following files:

capd/poincare/BasicPoincareMap.h
capd/poincare/BasicPoincareMap.hpp
capd/poincare/BasicPoincareMap_inline.h
capd/poincare/BasicPoincareMap_operator.hpp
capd/poincare/BasicPoincareMap_template.h

Public Types

Public Member Functions

Protected Member Functions

Protected Attributes

Detailed Description

template<typename SolverT, typename SectionT = AbstractSection<typename SolverT::MatrixType>> class capd::poincare::BasicPoincareMap< SolverT, SectionT >

Member Typedef Documentation

◆ CrossingDirection

◆ CurveType

◆ HessianType

◆ JetType

◆ MatrixType

◆ RealType

◆ ScalarType

◆ SectionType

◆ size_type

◆ SolutionCurve

◆ Solver

◆ VectorFieldType

◆ VectorType

Member Function Documentation

◆ operator()()

◆ setCrossingDirection()

Member Data Documentation

◆ m_blowUpMaxNorm

◆ m_crossingDirection

◆ m_maxReturnTime

◆ m_section

◆ m_sectionFactor

◆ m_solver

template<typename SolverT, typename SectionT = AbstractSection<typename SolverT::MatrixType>>
class capd::poincare::BasicPoincareMap< SolverT, SectionT >