The library consists of a large number of template functions and classes. For user convenience we provide two main header files in which most important types are defined. All defined types are located in the capd namespace.

#include "capd/capdlib.h"

Note: File "capd/capdlib.h" provides classes for computation in double and long double precision and in interval arithmetics based on double type.

#include "capd/mpcapdlib.h"

mpcapdlib.h

Multiple Precision version of CAPD library.

Note: File "capd/mpcapdlib.h" provides classes for computation in multiple precision floating numbers and in interval arithmetics of arbitrary precision.

Basic types and naming convention

In addition to the standard double and long double types, the above header files provide the following arithmetic types

capd::interval - interval aritghmetics based on standard double precision.
capd::MpFloat - arbitrary floating point arithmetics based of MPFR library
capd::MpInterval - interval arithmetics of arbitrary precission based on MpFloat type

On top of these five basic arithmetic types the CAPD library builds data structures such as vectors, matrices, hessians, jets (truncated Taylor series) and algorithms for manipulating them. Other data structures represent functions, solutions to ODEs or Poincaré maps, etc. Most of defined types use the following naming convention pattern

[Prefix]ClassName

where Prefix is one of the following

D – computation in floating points based on double standard type
LD – computation in floating points based on long double standard type
Mp – computation in floating points based on MpFloat
I – computation in interval arithmetics based on capd::interval type
MpI – computation in interval arithmetics based on capd::MpInterval type

For example

  DVector,   DMatrix,   DJet,   DMap,   DOdeSolver,   DPoincareMap, ...
 LDVector,  LDMatrix,  LDJet,  LDMap,  LDOdeSolver,  LDPoincareMap, ...
 MpVector,  MpMatrix,  MpJet,  MpMap,  MpOdeSolver,  MpPoincareMap, ...
  IVector,   IMatrix,   IJet,   IMap,   IOdeSolver,   IPoincareMap, ...
MpIVector, MpIMatrix, MpIJet, MpIMap, MpIOdeSolver, MpIPoincareMap, ...

List of the most important types

Here is (very incomplete) list of types provided for a user in "capd/capdlib.h" and "capd/mpcapdlib.h" header files.

[Prefix]Vector – vector or interval vector in Rⁿ
[Prefix]Matrix – matrix or interval matrix in R^n×m
[Prefix]Hessian – data structure to stores hessians of maps
[Prefix]Jet - data structure to stores jets (truncated Taylor series) of maps
[Prefix]EuclNorm, [Prefix]SumNorm, [Prefix]MaxNorm - various norms of vectors and matrices (operator norms).
[Prefix]Function - represents a multivariate, scalar valued function with vector arguments (can depend on parameters)
[Prefix]Map - represents a map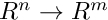 $R^n \to R^m$ . It can be used to define vector fields
[Prefix]OdeSolver - solver to ODEs based on the (high order) Taylor method or implict Hermite-Obreshkov method. The solver can integrate first order variational equations to ODEs.
[Prefix]CnOdeSolver - solver to ODEs based on the (high order) Taylor method. It can integrate higher order variational equations to ODEs.
[Prefix]TimeMap - computes solutions to ODEs over usually large time interval. It can integrate first order variational equations.
[Prefix]CnTimeMap - computes solutions to ODEs over the time interval. It can integrate higher order variational equations.
[Prefix]PoincareMap - computes Poincaré maps and their jacobians.
[Prefix]CnPoincareMap - computes Poincaré maps and their higher order derivatives.
[Prefix]NonlinearSection - most general Poincaré section of the form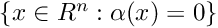 $\{x\in R^n : \alpha(x)=0\}$ , where 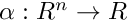$\alpha:R^n\to R$ is a smooth function
[Prefix]AffineSection - Poincaré section that is an affine hyperplane
[Prefix]CoordinateSection - Poincaré section that is of the form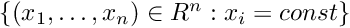 $\{(x_1,\ldots,x_n)\in R^n : x_i = const\}$

In the next chapters we will present basic usage of the above types.