Defined types and data structures

The main header file

defines the following types for computation in double (D), long double (LD) precision and interval (I) arithmetics.

DVector, LDVector, IVector - elements of 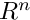in double and long double precision, and interval vectors
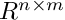
DMatrix, LDMatrx, IMatrix - matrices, elements and/or subsets of $R^{n\times m}$
DEuclNorm, LDEuclNorm, IEuclNorm - classes that compute Euclidean norm of vectors and matrices (operator norm).
DMaxNorm, LDMaxNorm, IMaxNorm - classes that compute max norm of vectors and matrices (operator norm)
DSumNorm, LDSumNorm, ISumNorm - classes that compute 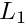norm of vectors and matrices (operator norm)

Vectors and matrices

Vectors and matrices are defined by a simple constructor calls

DVector v(4);  // four dimensional vector filled with zeroes
LDVector u(3); // three dimensional vector in long double precision  
IVector iv(6); // six dimensional interval vector filled with zeroes
 
DMatrix m(3,4);  // 3x4 matrix with coefficients set to zero
LDMatrix m(5,2);  // 5x2 matrix in long double precision with coefficients set to zero
IMatrix im(5,2); // 5x2 interval matrix with coefficients being intervals [0,0]  

Initialization of vectors and matrices:

interval vcoeff[] = {1.,2.,3.,4.,10.};
IVector v(5,vcoeff);
cout << v << endl;        // output: {[1,1],[2,2],[3,3],[4,4],[10,10]} 
 
double mcoeff[] = {1,2,3,4,5,6};
DMatrix m(2,3,mcoeff);
cout << m << endl;        // output: {{1,2,3},{4,5,6}} 
 
long double xcoeff[] = {1,2,3,4,5};
LDVector x(5,xcoeff);
cout << x << endl;        // output: {1,2,3,4,5} 

Note: Contructors of vectors and matrices assume that arrays of coefficients contain enough elements

Indexing of vectors and matrices

Vectors and matrices are indexed from zero by means of overloaded operator[].

IVector x(3);
x[0] = interval(3.);
x[1] = interval (1.,2.);
x[2] = 7.; // implicit conversion from double to interval
 
IMatrix m(2,4);
m[0][2] = interval(1.); 
m[1][3] = interval(2.,3.);
// m[2][4] = 1; // error - invalid indices

Note: Indexing of vectors and matrices starts from zero.

Arrays of vectors and matrices

When constructing arrays of matrices one has to provide two informations:

what is the length of array
what are dimensions of matrices/vectors in the array

If one wish to define array of matrices or vectors of the same dimensions we strongly encourage to use the following static funcitons

int dimension = 6;
int rows = 2, columns = 5;
int length = 3;
DVector* t = DVector::makeArray(length,dimension);
LDVector* p = DVector::makeArray(length,dimension);
IMatrix* m = IMatrix::makeArray(length,rows,columns);
 
// use the objects, like DVector x = t[0] + t[1]; etc
 
// and then release memory
 
delete []t;
delete []p;
delete []m;

Basic operations on vectors and matrices

Mathematical operators are overloaded wherever it is intuitive, like multiplications, additions, subtractions

IMatrix A(4,3), B(3,2);
IVector x(3), y(3);
 
IMatrix C = A*B;  // matrix by matrix multiplication
IVector u = A*x;  // matrix by vector multiplication
interval s = x*y; // scalar product of vectors
IVector v = 2.*u; // scalar by vector 
IVector z = x+y;  // vector addition
 
interval w = (x+y)*(x-y); // scalar product of (x+y) and (x-y)
// ... etc 

Basic algorithms of linear algebra.

Among others we provide algorithms for

transposition of matrices
solving linear systems
computing inverse matrices (inverting should be avoided if possible)
QR decomposition

DMatrix A(...);
DVector u(...);
DMatrix Q(...), R(...);
 
DMatrix B = transpose(A);             // transposition of matrix A
DMatrix invA = matrixAlgorithms::gaussInverseMatrix(A); // computation of inverse of A by means of Gauss algorithm 
DVector x = matrixAlgorithms::gauss(A,u);               // solves linear equations A*x = u.
matrixAlgorithms::QR_decompose(A,Q,R);                  // computes orthogonal matrix A and upper triagular R such that A = Q*R
 
IMatrix M(...);
IMatrix invM = matrixAlgorithms::krawczykInverse(M)     // computes enclosure of inverse of M       

Note: both functions gaussInverseMatrix and krawczykInverse compute enclosure of inverse of an interval matrix M. We recommend to use krawczykInverse as it always produces tighter enclosures.

Attention: In principle linear system could be solved by
// not recommended!

DVector x = gaussInverseMatrix(A)*u;

but this is much slower.

Note: The above functions throw an exception (object of type std::runtime_error) when they cannot finish operation.

Eigenvectors and eigenvalues of matrices

These functions are implemented for non-interval matrices only!. More information on this topic is given in section Non-rigorous computations of eigenvalues and eigenvectors.

Table of Contents