Chaos in the Rossler system

Consider the Rossler system

This example is a complete proof of

• the existence of an attractor A for the Rossler system with parameter values a=5.7, b=0.2.
• the existence of an uniformly hyperbolic invariant set H inside this attractor on which the dynamics is chaotic.

Let us fix Poincare section 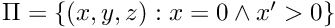and let 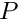be the associated Poincare map - see picture below.

The first assertion is proved by showing the existence of a trapping region for 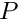. Namely, we show that the set

is mapped into itself by the Poincare map 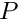, i.e. .

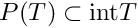The existence of chaotic dynamics has been proved for the first time by Piotr Zgliczyński

P. Zgliczyński,
Computer assisted proof of chaos in the Henon map and in the Rossler equations, 
Nonlinearity, 1997, Vol. 10, No. 1, 243--252

He introduced a new topological tool for proving the existence of periodic orbits and symbolic dynamics, named covering relations. These geometric conditions simply mean that the edges of a rectangle must be mapped by the function in a proper side of the other rectangle as presented on the picture below.

Uniform hyperbolicity is verified by means of the cone conditions criterion introduced in

H. Kokubu, D. Wilczak, P. Zgliczyński,
Rigorous verification of cocoon bifurcations in the Michelson system, 
Nonlinearity 20 (2007) 2147-2174.

The source of the program can be found in the capd/capdDynSys4/examples/RosslerChaoticDynamics directory of the CAPD library. The program runs within less than five seconds on a laptop-type computer. Most of the time is taken by the verification of the cone conditions.

Attention

This program requires C++11 compiler support, for instance gcc-4.8 or newer with -std=c++11 flag.

#include <iostream>
#include "capd/capdlib.h"
 
using namespace capd;
using namespace std;
 
// Coordinates of the trapping region of the attractor.
double g_bottom = 0.028;
double g_top = 0.034;
double g_left = -10.7;
double g_right = -2.3;
 
// Coordinates of sets on which symbolic dynamics is observed.
// M = [-8.4,-7.6]x[0.028,0.034]
// N = [-5.7,-4.6]x[0.028,0.034]
double g_leftM  = -8.4;
double g_rightM = -7.6;
double g_leftN  = -5.7;
double g_rightN = -4.6;
 
/*
 * A generic routine that checks
 * if the image under some iteration of Poincare map of the set
 *   [y1,y2]x[g_bottom,g_top]
 * satisfies condition 'c'.
 */
template<class Condition>
bool checkCondition(IPoincareMap& pm, double y1, double y2, int N, Condition c, int iteration = 2) {
  bool result = true;
  interval p = (interval(y2) - interval(y1)) / N;
  for (int i = 0; i < N; ++i) {
    IVector x = {interval(0.), y1 + interval(i,i+1) * p, interval(g_bottom, g_top)};
    C0HOTripletonSet s(x);
    IVector y = pm(s, iteration);
    result = result and c(y);
  }
  return result;
}
 
/*
 * This function checks if the matrix
 * DP^2(X)^T*Q*DP^2(X) - Q
 * is positive definite. Here Q = DiagMatrix{1,-100}. The set X is equal to M or N.
 */
 
bool checkConeCondition(IPoincareMap& pm, double y1, double y2, int N) {
  bool result = true;
  interval p = (interval(y2) - interval(y1)) / N;
  IMatrix monodromyMatrix(3,3);
  IMatrix quadraticForm(3,3);
  quadraticForm[1][1] = 1.;
  quadraticForm[2][2] = -100.;
  interval returnTime;
  for (int i = 0; i < N; ++i) {
    IVector x = {interval(0.), y1 + interval(i,i+1) * p, interval(g_bottom,g_top)};
    C1Rect2Set s = C1Rect2Set(x);
    IVector y = pm(s, monodromyMatrix, returnTime, 2);
    IMatrix DP = pm.computeDP(y,monodromyMatrix,returnTime);
    DP = Transpose(DP)*quadraticForm*DP - quadraticForm;
 
    result = result and DP[1][1]>0 and (DP[1][1]*DP[2][2]-sqr(DP[1][2]))>0;
  }
  return result;
}
 
int main() {
  cout << boolalpha;
  try {
    int order = 20;
    interval a = interval(57) / interval(10);
    interval b = interval(2) / interval(10);
    IMap vf("par:a,b;var:x,y,z;fun:-(y+z),x+b*y,b+z*(x-a);");
    vf.setParameter("a", a);
    vf.setParameter("b", b);
 
    IOdeSolver solver(vf, order);
    ICoordinateSection section(3, 0);
    IPoincareMap pm(solver, section, poincare::MinusPlus);
 
    // Lambda functions that check some inequalities.
    auto mappedLeft   = [] (IVector u) { return u[1] < g_leftM; };
    auto mappedRight  = [] (IVector u) { return u[1] > g_rightN; };
    auto mappedIn     = [] (IVector u) { return u[2] > g_bottom and u[2] < g_top and u[1] > g_left and u[1]<g_right; };
 
    // Here we check if [g_left,g_right]x[g_bottom,g_top] is mapped into itself by Poincare map.
    // From these computations we also obtain that the sets N and M are mapped across the horizontal strip.
    // This is one of the required conditions for the covering relations.
    cout << "Existence of attractor: " << checkCondition(pm, g_left, g_right, 200, mappedIn, 1) << endl;
 
    // Remaining inequalities for the covering relations N=>N, N=>M, M=>M, M=>N.
    cout << "P^2( Left (M) ) < Left (M): " << checkCondition( pm, g_leftM,  g_leftM,  1, mappedLeft  ) << endl;
    cout << "P^2( Right(M) ) > Right(N): " << checkCondition( pm, g_rightM, g_rightM, 1, mappedRight ) << endl;
    cout << "P^2( Left (N) ) > Right(N): " << checkCondition( pm, g_leftN,  g_leftN,  1, mappedRight ) << endl;
    cout << "P^2( Right(N) ) < Left (M): " << checkCondition( pm, g_rightN, g_rightN, 1, mappedLeft  ) << endl;
 
    // Check the cone conditions.
    cout << "Cone condition on the set M: " << checkConeCondition(pm,g_leftM,g_rightM,80) << endl;
    cout << "Cone condition on the set N: " << checkConeCondition(pm,g_leftN,g_rightN,40) << endl;
 
  } catch (exception& e) {
    cout << "\n\nException caught: " << e.what() << endl;
  }
  return 0;
}
 
// END