Defined types and data structures

The main header file

defines the following types for computation in double (D), long double (LD) precision and interval (I) arithmetics.

DFunction, LDFunction, IFunction - scalar valued functions $R^n\to R$
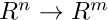
DMap, LDMap, IMap - vector valued maps $R^n\to R^m$
DHessian, LDHessian, IHessian - data structure to store second order normalized derivatives (Taylor coefficients) of maps
DJet, LDJet, IJet - data structure to store multivariate polynomials, i.e. truncated Taylor series of maps
Multiindex, Multipointer - data structures used to index jets.

Defining functions and maps

Maps can be parsed from a human readable string and/or C-routine. Performance of further computations does not depend on the way you define an object. This is for user convenience only - short functions can be defined as a string while large expressions are easier to encode as routines.

Parsing from a string. Syntax of the formula:

"[par:a,b,c...;][time:t;]var:x1,x2,...;fun:expression1,expression2,....;"

var - names of subsequent arguments
fun - expressions that define a map. You can use most elementary
- functions: sin, cos, exp, log, sqrt, sqr (square)
- operators: +,-,*,/,^ (power, integer or not. Exponent cannot depend on variables - we assume gradient of exponent is zero).
- constants: (0,1,2,-5,2.5,-0.25, etc)- we recommend usage of representable numbers only. If a constant is an interval or a floating point represented with high precision, one should use a parameter instead.
par - parameters of the map. Derivatives of them with respect to main variables are assumed to be zero.
time - a distinguished parameter with derivative dt/dt=1. Used to define time-dependent maps that stand for vector fields of nonautonomous ODEs.

Attention: The parser does not accept numerical constants in scientific notation. Use parameters, instead.

Note: Sections par and time are optional.

Example:

#include "capd/capdlib.h"
 
capd::IMap lorenz("par:s,r,q;var:x,y,z;fun:s*(y-x),x*(r-z)-y,x*y-q*z;");
lorenz.setParameter("s",10.);
lorenz.setParameter("r",28.);
lorenz.setParameter("q",interval(8.)/interval(3.));

Parsing from a C-routine. One has to write a global function (or a functor, lambda expression, can be class member function) that defines the map and then send it to the constructor of class Map.

The function that defines a map must have the following signature:

#include "capd/capdlib.h"
void vf(capd::autodiff::Node t,
        capd::autodiff::Node in[], int dimIn,
        capd::autodiff::Node out[], int dimOut,
        capd::autodiff::Node params[], int noParam
       );

Here:

t - is a distinguished time variable
in - is a C-array of input (independent) variables
dimIn - is number of input variables
out - is a C-array of output (dependent) variables
dimOut - is number of output variables
params - is a C-array of parameters
noParam - is number of parameters

See section Computing values and derivatives of maps for a complete example.

Computing values and derivatives of maps

Class Map provides methods for computation of values and derivatives. This is simply done by call to overloaded operator () and/or method derivative.

DMap f = ...;
DVector x = ...;
 
DVector y  = f(x);            // value of map f at x
DMatrix Df = f.derivative(x); // derivative of f at x
 
// much faster simultaneous computation of value and derivative
y = f(x,Df);  

Complete example (from examples/maps/mapExample.cpp):

#include <iostream>
#include "capd/capdlib.h"
 
using namespace capd;
using namespace std;
using capd::autodiff::Node;
 
// ####################################################
 
/*
 * This is a map we will evaluate and differentiate - vector field of the PCR3BP
 * @param in - an array of independent variables
 * @param out - an array of dependent variables, i.e. out = f(in)
 * @param params - parameters of the map. Here we assume that mu=params[0] is a relative mass of Jupiter
 */
void pcr3bpVectorField(Node /*t*/, Node in[], int /*dimIn*/, Node out[], int /*dimOut*/, Node params[], int /*noParams*/)
{
  // Try to factorize expression as much as possible.
  // Usually we have to define some intermediate quantities.
 
  Node mj = 1-params[0]; // relative mass of the Sun
  Node xMu = in[0] + params[0];
  Node xMj = in[0] - mj;
  Node xMuSquare = xMu^2; // square
  Node xMjSquare = xMj^2;
  Node ySquare = in[1]^2;
 
  // power -1.5, for rigorous computation use ONLY REPRESENTABLE CONSTANTS.
  // If exponent is not representable or it is an interval then it should be a parameter of the map.
  Node factor1 = mj*((xMuSquare+ySquare)^-1.5);
  Node factor2 = params[0]*((xMjSquare+ySquare)^-1.5);
 
  out[0] = in[2];
  out[1] = in[3];
  out[2] = in[0] - xMu*factor1 - xMj*factor2 + 2*in[3];
  out[3] = in[1]*(1 - factor1 - factor2) - 2*in[2];
}
 
// ####################################################
 
int main(){
  cout.precision(21); // 21 digits of output in long double precision
 
  int dimIn=4, dimOut=4, noParam=1;
  LDMap f(pcr3bpVectorField,dimIn,dimOut,noParam);
 
  // set value of parameters mu, which is relative mass of Jupiter
  // 0 is index of parameter, 0.125 is its new value
  f.setParameter(0, 0.125);
 
  long double v[] = {2,3,4,5};
  LDVector x(dimIn,v);
 
  LDVector y = f(x);
  LDMatrix Df = f.derivative(x);
 
  cout << "f(x)=" << y << endl;
  cout << "Df(x)=" << Df << endl;
 
  // simultaneous computation of value and derivative - much faster
  LDMatrix Df2(dimOut,dimIn);
  LDVector y2 = f(x,Df2);
 
  // check the result
  cout << "y-y2=" << y-y2 << endl;
  cout << "Df-Df2=" << Df-Df2 << endl;
}
 
// ####################################################
 
/* output:
f(x)={4,5,11.9583037484840325037,-5.06423059909286367008}
Df(x)={
{0,0,1,0},
{0,0,0,1},
{0.997645929251066642188,0.0286667054591395971705,0,2},
{0.0286667054591395971722,1.02376427044655458117,-2,0}
}
y-y2={0,0,0,0}
Df-Df2={
{0,0,0,0},
{0,0,0,0},
{0,0,0,0},
{0,0,0,0}
*/

Attention

For rigorous computation you must use in the expression representable numbers only (both in the string parsed and routine parsed cases). If you want to use constants, like 1/3 then you can

either set them as parameters of the system (strongly recommended) - do not forget to set the parameter value after creating an instance of Map.
or wrap them into Node type (slower):
Node(1)/Node(3)

String parser wraps automatically expressions like 1/3 to division of nodes.

Hessians of maps

Class Map provides algorithms for computation of normalized hessians of maps. One has to

set maximal order of derivative to at least 2, when creating an instance of Map
DMap f(globalFunction,dimIn,dimOut,noParams,maxDerivative /*at least 2*/);

globalFunction
void globalFunction()
Definition: Example.h:38
define objects that will store computed derivative and hessian
DVector x = ...;

DMatrix Df(dimOut,dimIn);

DHessian Hf(dimOut,dimIn);

capd::DHessian
capd::diffAlgebra::Hessian< capd::DVector::ScalarType, capd::DVector::csDim, capd::DMatrix::ColumnVectorType::csDim > DHessian
Definition: fdlib.h:40
call operator ()
DVector fx = f(x,Df,Hf);

Now Hf stores second order normalized derivatives. They can be accessed by

int fi =..., dxj = ..., dxk = ...;

double dfi_dxj_dxk = Hf(fi,dxj,dxk);

Note: Indexing of functions (fi) and derivatives (dxj,dxk) starts from zero.

Complete example (from examples/maps/hessianExample.cpp):

 
#include <iostream>
#include "capd/capdlib.h"
 
using namespace capd;
using namespace std;
using capd::autodiff::Node;
 
// ####################################################
 
/*
 * This is a map we will evaluate and differentiate (dimIn = 4, dimOut = 2, noParams = 5)
 * @param in is an array of independent variables
 * @param out is an array of dependent variables, i.e. out = f(in)
 * @param params - parameters of the map.
 */
void _f(Node /*t*/, Node in[], int /*dimIn*/, Node out[], int /*dimOut*/, Node params[], int noParams)
{
  out[0] = in[0]+in[1];
  out[1] = -(in[2]+in[3]);
 
  for(int i=0;i<noParams;++i){
    Node temp = params[i]*sqrt(sqr(out[0] - in[0]) + sqr(out[1] - in[3]));
    out[1] = params[i]*sqrt(sqr(out[0] + in[1]) + sqr(out[1] - in[2]));
    out[0] = temp;
  }
}
 
// ####################################################
 
int main(){
  int dimIn=4, dimOut=2, noParam=5;
 
  // this is the maximal order of derivative we request
  // default value is set to 1 if the argument is skipped
  int maxDerivativeOrder = 2;
  IMap f(_f,dimIn,dimOut,noParam,maxDerivativeOrder);
 
  // set parameter value that encloses 1/9, 2/9, etc
  for(int i=0;i<noParam;++i)
    f.setParameter(i, interval(i+1)/interval(9));
 
  interval v[] = {2,3,4,5};
  IVector x(dimIn,v);
 
  // declare an object for storing derivative and hessian
  IMatrix Df(dimOut,dimIn);
  IHessian Hf(dimOut,dimIn);
 
  // simultaneous computation of value, derivative and normalized hessian
  // NOTE! Hf contains second order Taylor coefficients of f at x, i.e. normalized derivatives.
  IVector y = f(x,Df,Hf);
 
  // print value and derivative of f at x
  cout.precision(17);
  cout << "y=" << y << endl;
  cout << "Df=" << Df << endl;
 
  // print normalized second order derivatives
  for(int fi=0;fi<dimOut;++fi)
    for(int dx1=0;dx1<dimIn;++dx1)
      for(int dx2=dx1;dx2<dimIn;++dx2)
        cout << "Hf(" << fi << "," << dx1 << "," << dx2 << ")=" << Hf(fi,dx1,dx2) << endl;
}
 
// ####################################################
 
/* output:
y={[1.5666313012267541, 1.5666313012267572],[2.7160497654235312, 2.7160497654235356]}
Df={
{[0.060484484806883045, 0.060484484806884051],[-0.16642557749344458, -0.16642557749344236],[-0.086398550591301623, -0.086398550591300416],[0.45810665329170269, 0.45810665329170663]},
{[0.029096263766104483, 0.02909626376610501],[0.40574188883571083, 0.40574188883571372],[0.13126754262517129, 0.13126754262517268],[0.18311228017669873, 0.18311228017670086]}
}
Hf(0,0,0)=[0.074118944476562462, 0.074118944476563184]
Hf(0,0,1)=[0.021315780883087665, 0.021315780883088681]
Hf(0,0,2)=[0.01769262837118854, 0.017692628371189165]
Hf(0,0,3)=[-0.08623872680805543, -0.086238726808053057]
Hf(0,1,1)=[-0.0053748330978258384, -0.0053748330978252252]
Hf(0,1,2)=[0.019554811781480465, 0.019554811781482002]
Hf(0,1,3)=[-0.017720362061031517, -0.017720362061027721]
Hf(0,2,2)=[-0.0091193387205848984, -0.0091193387205845741]
Hf(0,2,3)=[-0.004218996464429756, -0.0042189964644276561]
Hf(0,3,3)=[0.024251452565690394, 0.024251452565692031]
Hf(1,0,0)=[0.020245143945059545, 0.020245143945059847]
Hf(1,0,1)=[0.0087801679885119114, 0.0087801679885125602]
Hf(1,0,2)=[-0.0021131490236710707, -0.0021131490236707558]
Hf(1,0,3)=[-0.019773696730218816, -0.019773696730217935]
Hf(1,1,1)=[0.015870027950691565, 0.015870027950692377]
Hf(1,1,2)=[-0.04225008508394984, -0.042250085083948029]
Hf(1,1,3)=[0.01124396733092266, 0.011243967330925161]
Hf(1,2,2)=[0.028717542333811172, 0.028717542333811609]
Hf(1,2,3)=[-0.019752757074261142, -0.019752757074259841]
Hf(1,3,3)=[0.0084826519764703637, 0.0084826519764710315]
*/

Higher order Taylor coefficients of maps

Class Map provides algorithms for computation of normalized higher order derivatives of maps. One has to

set maximal order of derivative to desired value, when creating an instance of Map
DMap f(globalFunction,dimIn,dimOut,maxRequestedDerivative /*default is 1*/);
define objects that will store jets of maps. Class [L]DJet (and interval version IJet) represents truncated Taylor series of a map.
DVector x = ...;

DJet fJet(dimOut,dimIn,truncationDegreeInclusive /*should be less or equal to maxRequestedDerivative*/);

capd::DJet
capd::diffAlgebra::Jet< capd::DMatrix, 0 > DJet
Definition: fdlib.h:44
call operator ()
f(x,fJet);

Now fJet stores value of f(x) and all normalized derivatives of f at x up to order truncationDegreeInclusive. For partial derivatives of order less or equal than three we provide direct access to coefficients by simple operator call

int fi =..., dxj = ..., dxk = ..., dxc = ...;
 
DVector fx = fJet();                           // value of f(x)
double dfi_dxj = fJet(fi,dxj);                 // first order derivative
double dfi_dxj_dxk = fJet(fi,dxj,dxk);         // second order derivative 
double dfi_dxj_dxk_dxc = fJet(fi,dxj,dxk,dxc); // third order derivative

Note: Indexing of functions (fi) and derivatives (dxj,dxk) starts from zero.

Attention: For performance reasons indices in fJet(fi,dxj,dxk,dxc) must form a nondecreasing sequence! Otherwise behaviour is undefined.

Complete example (from examples/maps/jetExample.cpp):

 
#include <iostream>
#include "capd/capdlib.h"
 
using namespace capd;
using namespace std;
using capd::autodiff::Node;
 
// ####################################################
 
/*
 * This is a map we will evaluate and differentiate (dimIn = 3, dimOut = 2, noParams = 5)
 * @param in is an array of independent variables
 * @param out is an array of dependent variables, i.e. out = f(in)
 * @param params - parameters of the map.
 */
void _f(Node /*t*/, Node in[], int /*dimIn*/, Node out[], int /*dimOut*/, Node params[], int noParams)
{
  out[0] = in[0]+in[1];
  out[1] = -(in[1]+in[2]);
 
  for(int i=0;i<noParams;++i){
    Node temp = params[i]*sqrt(sqr(out[0] - in[1]) + sqr(out[1] - in[2]));
    out[1] = params[i]*sqrt(sqr(out[0] + in[2]) + sqr(out[1] - in[0]));
    out[0] = temp;
  }
}
 
// ####################################################
 
int main(){
  int dimIn=3, dimOut=2, noParam=5;
 
  // this is the maximal order of derivative we request
  // default value is set to 1 if the argument is skipped
  int maxDerivativeOrder = 3;
  DMap f(_f,dimIn,dimOut,noParam,maxDerivativeOrder);
 
  // set parameter values
  for(int i=0;i<noParam;++i)
    f.setParameter(i, double(i+1)/9.);
 
  double v[] = {2,3,4};
  DVector x(dimIn,v);
 
  // declare an object for storing jets
  DJet jet(dimOut,dimIn,maxDerivativeOrder);
  f(x,jet);
 
  // print the result
  // NOTE: indices of variables must form a nondecreasing sequence!
  cout << "df1_dx0_dx0_dx2 = " << jet(1,0,0,2) << endl;
 
 
  cout << jet.toString();
}
 
// ####################################################
 
/* output:
df1_dx0_dx0_dx2 = -0.0066946
 
value :
   {0,0,0}  : {1.31271,2.96826}
Taylor coefficients of order 1 :
   {1,0,0}  : {-0.00665595,-0.041866}
   {0,1,0}  : {0.279001,0.116691}
   {0,0,1}  : {0.122254,0.67548}
Taylor coefficients of order 2 :
   {2,0,0}  : {-0.00986967,0.0438603}
   {1,1,0}  : {0.00505905,-0.00594214}
   {1,0,1}  : {0.00607538,-0.0394037}
   {0,2,0}  : {0.0322789,0.0145537}
   {0,1,1}  : {-0.0509478,-0.0188595}
   {0,0,2}  : {0.0175866,0.0169232}
Taylor coefficients of order 3 :
   {3,0,0}  : {0.00112803,-0.00261786}
   {2,1,0}  : {0.00424835,-0.000458252}
   {2,0,1}  : {-0.00241089,-0.0066946}
   {1,2,0}  : {-0.000898502,-0.000433624}
   {1,1,1}  : {-0.00416536,0.00259422}
   {1,0,2}  : {0.00200803,0.00729993}
   {0,3,0}  : {-0.0088823,-0.00260142}
   {0,2,1}  : {0.0123647,0.00243158}
   {0,1,2}  : {-0.0018637,-0.000114807}
   {0,0,3}  : {-0.0013343,-0.00259822}
*/

Indexing of higher order derivatives

Fourth and higher order derivatives are indexed by multipointers and multiindices.

Multiindex: is an element of (sequence of integers) of the same length as the dimension of the domain of function, i.e. .

i-th coefficient of a multiindex indicates the order of partial derivative with respect to i-th variable. For instance,

int data[] = {2,1,0,2};

Multiindex m(4,data);

capd::Multiindex

capd::vectalg::Multiindex Multiindex

Definition: typedefs.h:60

corresponds to normalized derivative

Multipointer: is a nondecreasing sequence of integers of the length d, where d is the total order of partial derivative. Every element of multipointer is an index of variable with respect to which we take partial derivative. For instance, the following Multipointer

int data[] = {0,0,1,3,3};

Multipointer m(5,data);

capd::Multipointer

capd::vectalg::Multipointer Multipointer

Definition: typedefs.h:61

is equivalent to Multiindex {2,1,0,2} and it corresponds to normalized derivative

Given multipointer or multiindex one can access corresponding coefficient in the data structure Jet. One can also easily convert between multipointers and multiindices by constructor calls.

Complete example (from examples/maps/jetIndexingExample.cpp):

 
#include <iostream>
#include "capd/capdlib.h"
 
using namespace capd;
using namespace std;
using capd::autodiff::Node;
 
// ####################################################
 
/*
 * This is a map we will evaluate and differentiate (dimIn = 3, dimOut = 2, noParams = 5)
 * @param in is an array of independent variables
 * @param out is an array of dependent variables, i.e. out = f(in)
 * @param params - parameters of the map.
 */
void _f(Node /*t*/, Node in[], int /*dimIn*/, Node out[], int /*dimOut*/, Node params[], int noParams)
{
  out[0] = in[0]+in[1];
  out[1] = -(in[1]+in[2]);
 
  for(int i=0;i<noParams;++i){
    Node temp = params[i]*sqrt(sqr(out[0] - in[1]) + sqr(out[1] - in[2]));
    out[1] = params[i]*sqrt(sqr(out[0] + in[2]) + sqr(out[1] - in[0]));
    out[0] = temp;
  }
}
 
// ####################################################
 
int main(){
  int dimIn=3, dimOut=2, noParam=5;
 
  // this is the maximal order of derivative we request
  // default value is set to 1 if the argument is skipped
  int maxDerivativeOrder = 4;
  DMap f(_f,dimIn,dimOut,noParam,maxDerivativeOrder);
 
  // set parameter values
  for(int i=0;i<noParam;++i)
    f.setParameter(i, double(i+1)/9.);
 
  double v[] = {2,3,4};
  DVector x(dimIn,v);
 
  // declare an object for storing jets
  DJet jet(dimOut,dimIn,maxDerivativeOrder);
  // compute partial derivatives
  f(x,jet);
 
  // print the result
  int data[] = {0,2,2};
  Multiindex m(3,data);
  cout << "multiindex: " << m << endl;
 
  cout << "vector of Taylor coefficients D^{m}f = " << jet(m) << endl;
  cout << "selected Taylor coefficient D^{m}f_1 = " << jet(1,m) << endl << endl;
 
  Multipointer mp(m);
  cout << "conversion to multipointer: " << mp << endl;
  cout << "vector of Taylor coefficients D^(mp}f = " << jet(m) << endl;
  cout << "selected Taylor coefficient D^(mp}f_1 = " << jet(1,m) << endl << endl;
 
  // print all Taylor coefficients of degree 4
  Multipointer p = jet.first(4);
  do{
    cout << p << ": " << jet(p) << endl;
  }while(jet.hasNext(p));
  return 0;
}
 
// ####################################################
 
/* output:
multiindex: {0,2,2}
vector of Taylor coefficients D^{m}f = {-0.00197489,-0.000377739}
selected Taylor coefficient D^{m}f_1 = -0.000377739
 
conversion to multipointer: {1,1,2,2}
vector of Taylor coefficients D^(mp}f = {-0.00197489,-0.000377739}
selected Taylor coefficient D^(mp}f_1 = -0.000377739
 
{0,0,0,0}: {6.64042e-05,6.03996e-05}
{0,0,0,1}: {-0.000418493,0.000195404}
{0,0,0,2}: {-0.000382953,0.00104158}
{0,0,1,1}: {-0.00100131,-0.00011813}
{0,0,1,2}: {5.53662e-06,0.000113215}
{0,0,2,2}: {0.00088786,0.000850009}
{0,1,1,1}: {-8.04876e-05,0.000219013}
{0,1,1,2}: {0.00163166,-0.000157837}
{0,1,2,2}: {-0.000185176,-0.000586786}
{0,2,2,2}: {-0.000584331,-0.00135329}
{1,1,1,1}: {0.00194541,0.00045357}
{1,1,1,2}: {-0.00135485,-0.000169508}
{1,1,2,2}: {-0.00197489,-0.000377739}
{1,2,2,2}: {0.00132892,0.000305802}
{2,2,2,2}: {-9.34493e-06,0.000436602}
*/

Jet transport - computing composition of jets

Class Map defines an operator for computating jet of a composition of the map and other jet sent as an argument. Given map f

DMap f = ...;

and jet g at a point x

DJet g(...);

g(i,j,k) = ...; // fill the jet by data

one can compute jet of f(g(x)) by simply call

DJet f_of_g_at_x = f(g);

Complete example (from examples/maps/jetTransportExample.cpp):

 
#include <iostream>
#include "capd/capdlib.h"
 
using namespace capd;
using namespace std;
using capd::autodiff::Node;
 
// ####################################################
 
/*
 * This is a map we will evaluate and differentiate (dimIn = 2, dimOut = 2, noParams = 0)
 * @param in is an array of independent variables
 * @param out is an array of dependent variables, i.e. out = f(in)
 * @param params - parameters of the map.
 */
void _f(Node /*t*/, Node in[], int /*dimIn*/, Node out[], int /*dimOut*/, Node /*params*/[], int/* noParams*/)
{
  Node d = sqr(in[0])+sqr(in[1]);
  out[0] = (sqr(in[0])+in[1])/d;
  out[1] = (sqr(in[1])+in[0])/d;
}
 
// ####################################################
 
int main(){
  int dimIn=2, dimOut=2, noParam=0;
 
  // this is the maximal order of derivative we request
  int maxDerivativeOrder = 3;
  DMap f(_f,dimIn,dimOut,noParam,maxDerivativeOrder);
 
  double v[] = {2,3};
  DVector x(dimIn,v);
 
  // declare an object for storing jets
  DJet fx(dimOut,dimIn,maxDerivativeOrder);
 
  // and compute jet of f(x);
  f(x,fx);
  cout << "f(x):\n" << fx.toString() << endl;
 
  // now we compute jet of f(f(x))
  DJet ffx = f(fx);
  cout << "f(f(x)):\n" << ffx.toString();
  return 0;
}
 
// ####################################################
 
/* output:
f(x):
 
value :
   {0,0}  : {0.538462,0.846154}
Taylor coefficients of order 1 :
   {1,0}  : {0.142012,-0.183432}
   {0,1}  : {-0.171598,0.0710059}
Taylor coefficients of order 2 :
   {2,0}  : {-0.00819299,-0.00864816}
   {1,1}  : {-0.0127447,0.0628129}
   {0,2}  : {0.0377788,-0.0209376}
Taylor coefficients of order 3 :
   {3,0}  : {-0.00840307,0.0167711}
   {2,1}  : {0.0209026,-0.0207976}
   {1,2}  : {-0.0166661,-0.00843808}
   {0,3}  : {-0.00423655,0.00420153}
 
f(f(x)):
 
value :
   {0,0}  : {1.12941,1.24706}
Taylor coefficients of order 1 :
   {1,0}  : {0.146505,0.0278201}
   {0,1}  : {-0.0405536,0.0289965}
Taylor coefficients of order 2 :
   {2,0}  : {-0.0084657,-0.0225223}
   {1,1}  : {-0.0165577,0.0513845}
   {0,2}  : {0.00167963,-0.0400586}
Taylor coefficients of order 3 :
   {3,0}  : {-0.023039,-0.00636561}
   {2,1}  : {0.0387984,0.0137109}
   {1,2}  : {-0.0165008,-0.0181941}
   {0,3}  : {0.00349705,0.0127827}
*/

Table of Contents