Table of Contents
Defined types and data structures
The main header file
defines the following types for computation in (I) interval arithmetics.
- IOdeSolver - ODE solver, it can integrate first order variational equations
- IC2OdeSolver - ODE solver, it can integrate first and second order variational equations
- ICnOdeSolver - ODE solver, it can integrate higher order variational equations
- C0Rect2Set, C0HORect2Set - doubleton representation of a subset of
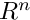 (see Representation of initial condition)
(see Representation of initial condition) - C0TripletonSet, C0HOTripletonSet - tripleton representation of a subset of
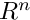 (see Representation of initial condition)
(see Representation of initial condition) - ITimeMap - integrates ODE over a time interval. It can integrate first and second order variational equations.
- IC2TimeMap - integrates ODE over a time interval. It can integrate first and second order variational equations.
- ICnTimeMap - integrates ODE over a time interval. It can integrate higher order variational equations.
Moreover, every class [Prefix]TimeMap defines public type SolutionCurve that is a functional object representing solution to IVP over time range. For example,
The CAPD library implements three strategies for solving IVP for ODEs. One can choose from
- one-step numerical scheme based on high-order Taylor method or explicit-implicit Hermite-Obreshkov method
- a method for computation of the solution after a given time. This approach combines one-step scheme with automatic step control.
- a method for computation of a solution curve (as a functional object) over a time range.
Before we describe these strategies in details we need to explain how subsets of phase space are represented in the memory of a computer.
Representation of initial condition
The CAPD library provides various methods for rigorous enclosures of trajectories. There are two main groups of rigorous solvers
- based on Taylor method
- based on Hermite-Obreshkov (explicit-implicit) method
In each group we implemented several algorithms with performance depending on dynamical properties of the system in consideration. In this section we will present four main algorithms that proved to be most efficient in typical cases.
The rigorous solver IOdeSolver requires that the initial condition is given in one of the acceptable representation. Among others four of them are proved to be most efficient and thus we omit other in this introduction. These are defined in classes
- C0Rect2Set, C0TripletonSet
- C0HORect2Set, C0HOTripletonSet
Two classes C0Rect2Set and C0HORect2Set represent a subset of ![]() in the form of doubleton
in the form of doubleton ![]() where
where
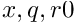 are interval vectors, where
are interval vectors, where 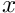 is a point interval vector
is a point interval vector 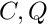 are interval matrices, with
are interval matrices, with 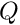 close to orthogonal
close to orthogonal
Two classes C0TripletonSet and C0HOTripletonSet represent a subset of ![]() in the form of tripleton
in the form of tripleton ![]() where
where
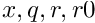 are interval vectors, where
are interval vectors, where 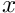 is a point interval vector
is a point interval vector 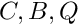 are interval matrices, with
are interval matrices, with 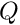 close to orthogonal
close to orthogonal
They differ by the numerical method used to integrate an ODE:
- C0Rect2Set and C0TripletonSet use high order Taylor method
- C0HORect2Set and C0HOTripletonSet use high order Taylor method as a predictor and then Hermite-Obreshkov implicit method as a corrector step
One can define an instance of these classes by simple contructor call
If the initial condition is not an interval vector but an affine set
![]()
we strongly recommend to use one of the following overloaded constructors
All above classes provide conversion to interval vector:
One-step method
Given an initial condition set (which is an instance of either C0Rect2Set or C0HORect2Set or C0TripletonSet or C0HOTripletonSet) one can compute image of this set after one step of numerical method. One has to
- create an instance of IOdeSolver
- propagate the set by the solver The solver makes automatic time step prediction (provided it has not been turned off by the user) and computes rigorous bound of this set after one time step. Internally, the set holds doubleton or tripleton representation of a subset ofset.move(solver);
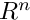 that is ready to perform the next time step.
that is ready to perform the next time step.
As in the case of nonrigorous computation the user can fix time step by the call to
- Note
- After fixing time step the solver tries to validate the existence of solutions over this time and for the set of initial conditions represented by
set.An exception is thrown if the solver cannot validate the existence of solution over time rangeset.move(solver);[0,timeStep].
One-step method, although possible, is not recommended in general. Sometimes it performs better for very wide initial conditions with relatively low order of the method (3-5). For long-time integration we recommend to use class ITimeMap that combines ISolver with automatic step control strategies.