Table of Contents
Representation of initial condition
The rigorous solver requires that the initial condition for variational equations is given in one of the acceptable representation. We have implemented several algorithms and representations but C1Rect2Set and C1HORect2Set proved to be most efficient in most typical applications.
These classes represent a subset of ![]() in the form of doubleton
in the form of doubleton ![]() where
where
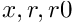 are interval vectors,
are interval vectors, 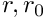 contain zero
contain zero 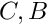 are interval matrices, with
are interval matrices, with 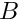 close to orthogonal
close to orthogonal
They represent monodromy matrix also in the form of doubleton ![]() where
where
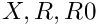 are interval matrices,
are interval matrices, 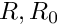 contain zero
contain zero 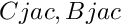 are interval matrices, with
are interval matrices, with 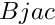 close to orthogonal
close to orthogonal
One can define an instance of C1Rect2Set or C1HORect2Set by constructor call
- Note
- initialTime can be skipped and then it is set to zero
- Note
- the above constructor sets Identity as the initial condition for variational equations
If the initial condition is not an interval vector but an affine set
![]()
we recommend to use one of the following overloaded constructors
Long-time integration of variational equations
The class TimeMap (see Long-time integration) provides interface for long-time integration of ODEs with associated variational equations. One has to specify initial condition
and call suitable operator
After successful integration one can extract monodromy matrix from the object set
- Note
- When solving ODEs with variational equations step control mechanism predicts time steps to fix requested error tolerances both for main equations and for variational equations.
Below is an example of integration of the forced pendulum equation.
See also an example of integration of the Rossler system with variational equations: Integration of ODE along with a variational equations
Complete example (from examples/odes/ITimeMapVariationalEquationsExample.cpp):
Variational equations - functional approach
As in the case of computing trajectories (see Solutions to IVPs as functions) one can obtain solution to variational equation as a functional object that can be evaluated at any intermediate time.
Complete example (from examples/odesrig/ITimeMapMonodromyMatrixCurveExample.cpp):