Long-time integration

Table of Contents

• Computing solution after fixed time
• Computing intermediate points on the trajectory
• Error tolerance and step control

The best way to compute long pieces of trajectory is to use two classes together: DOdeSolver with DTimeMap or LDOdeSolver with LDTimeMap. The class [L]DTimeMap provides interface for computing trajectories over time range and/or variational equations hiding all technical details. Using this approach one can

• manage parameters of step control methods (like relative and absolute tolerances)
• compute intermediate points that appeared during integration (we will call this dense output)
• compute solutions to IVPs as functional objects

Computing solution after fixed time

This is the simplest and perhaps most often used feature of class TimeMap. In order to compute a solution to ODE after a specified time T one should

• create an instance of ODE solver as described in section One-step Taylor method

  DOdeSolver solver(...); 

• create an instance of DTimeMap

  DTimeMap timeMap(solver); 

• specify initial condition and integrate over the given time

  double initialTime = ....;
  double finalTime = ...;
  DVector u(...);
   
  DVector y = timeMap(finalTime,u,initialTime);

After the last call we obtain where is local flow induced by our ODE. Complete example will be given in section Error tolerance and step control

Note

After integration initialTime will be updated to finalTime

Attention

This is integration over time finalTime-initialTIme and not over finalTime.

Note

For autonomous systems the last argument (initialTime) can be skipped.

DVector y = timeMap(finalTime,u);

Computing intermediate points on the trajectory

One can stop long-time integration after each performed time step. This can be obtained by the following request before starting integration

timeMap.stopAfterStep(true);

Then we can use the following loop to integrate over a given time

double initialTime = ....;
double finalTime = ...;
DVector u(...);
 
do{
  DVector y = timeMap(finalTime,u,initialTime);
  cout << "current time=" << timeMap.getCurrentTime() <<  ", y=" << y << endl; 
}while(!timeMap.completed());

Complete example (from examples/odes/DTimeMapExample.cpp):

#include <cstdio>
#include "capd/capdlib.h"
 
using namespace capd;
 
int main(){
  // define an instance of class DMap that describes the vector field
  DMap pendulum("time:t;par:omega;var:x,dx;fun:dx,sin(omega*t)-sin(x);");
  pendulum.setParameter("omega",1.);
 
  int order = 30;
  DOdeSolver solver(pendulum,order);
  DTimeMap timeMap(solver);
 
  // specify initial condition
  DVector u(2);
  u[0] = 1.;
  u[1] = 2.;
  double initTime = 4;
  double finalTime = 8;
 
  // use Taylor method with step control to integrate
  timeMap.stopAfterStep(true);
 
  do{
    u = timeMap(finalTime,u,initTime);
    printf("t=%6f, x=%6f, dx=%6f\n",initTime,u[0],u[1]);
  }while(!timeMap.completed());
 
  return 0;
}
 
/* output:
t=4.343750, x=1.584065, dx=1.379298
t=4.718750, x=1.964273, dx=0.649367
t=5.171875, x=2.065724, dx=-0.190317
t=5.703125, x=1.723517, dx=-1.077336
t=6.125000, x=1.143133, dx=-1.641492
t=6.500000, x=0.469677, dx=-1.898192
t=6.875000, x=-0.234645, dx=-1.793385
t=7.234375, x=-0.809953, dx=-1.363382
t=7.609375, x=-1.202215, dx=-0.706059
t=8.000000, x=-1.329739, dx=0.056758
*/

Error tolerance and step control

Let be the error of numerical method that approximates exact solution . The class [L]DOdeSolver makes a prediction of time step subject to fix constrains on local errors per unit step. These constraints are standard

• absolute tolerance 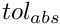- we require that 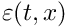is smaller than this quantity (usually we require that the max norm of the Lagrange remainder in the Taylor series is less than absolute tolerance).
  
• relative tolerance 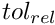- we require that 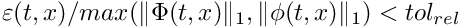. This condition is technically difficult to check in the prediction of the time step.
  Therefore we assume that the denominator is evaluated for t=0 only, and compute time step subject to constrain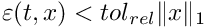

Eventually, the time step is computed subject to

The user can change default values of tolerances or even turn off step control by means of the following methods

DMap vectorField(...);  
int order = ...;
 
// by default step control is turned on
DOdeSolver solver(vectorFiels,order);
DTimeMap timeMap(solver);
 
// turning off step control results in integration with fixed time step timeStep
double timeStep = ...;
solver.setStep(timeStep);
 
// one can turn on step control at any moment
solver.turnOnStepControl();
 
// one can change tolerances at any moment. 
// For low orders of the Taylor method we recommend to change default values. 
double absoluteTolerance = ...;
double relativeTolerance = ...;
solver.setAbsoluteTolerance(absoluteTolerance); 
solver.setRelativeTolerance(relativeTolerance);

Attention

Using low orders of the Taylor method with very small tolerances usually forces very small time steps and thus integration might be slow.

Complete example (from examples/odes/DTimeMapStepControlExample.cpp):

#include <cstdio>
#include "capd/capdlib.h"
 
using namespace capd;
 
void integrate(DTimeMap& timeMap){
  // Specify initial condition
  DVector u(2);
  u[0] = 1.;
  u[1] = 2.;
  double initTime = 0;
  double finalTime = 100;
  int stepsCounter = 0;
 
  timeMap.stopAfterStep(true);
  do{
    u = timeMap(finalTime,u,initTime);
    stepsCounter++;
  }while(!timeMap.completed());
  printf("x=%.10f, dx=%.10f\n",u[0],u[1]);
  printf("order=%d, steps=%d\n\n",timeMap.getSolver().getOrder(),stepsCounter);
}
 
int main(){
  // Define an instance of class DMap that describes the vector field
  DMap pendulum("time:t;par:omega;var:x,dx;fun:dx,sin(omega*t)-sin(x);");
  pendulum.setParameter("omega",1.);
 
  // Define an instance of ODE solver and TimeMap
  int order = 20;
  DOdeSolver solver(pendulum,order);
  DTimeMap timeMap(solver);
 
  printf("------- Integration of pendulum over time range 0-100 -----------------\n\n");
 
  double step = 0.125;
  solver.setStep(step);
  printf("Constant time step %f:\n",step);
  integrate(timeMap);
 
  timeMap.turnOnStepControl();
  printf("Default step control and default tolerance:\n");
  integrate(timeMap);
 
  // change order
  solver.setOrder(10);
  printf("Default step control and default tolerance:\n");
  integrate(timeMap);
 
  // change tolerance
  double tol = 1e-8;
  solver.setAbsoluteTolerance(tol);
  solver.setRelativeTolerance(tol);
  printf("Default step control with absolute and relative tolerances set to %.1e:\n",tol);
  integrate(timeMap);
 
  // change order
  solver.setOrder(20);
  printf("Default step control with absolute and relative tolerances set to %.1e:\n",tol);
  integrate(timeMap);
 
  return 0;
}
 
/* output:
------- Integration of pendulum over time range 0-100 -----------------
 
Constant time step 0.125000:
x=256.1915412352, dx=1.9673787155
order=20, steps=800
 
Default step control and default tolerance:
x=256.1915412353, dx=1.9673787155
order=20, steps=518
 
Default step control and default tolerance:
x=256.1915412354, dx=1.9673787156
order=10, steps=4677
 
Default step control with absolute and relative tolerances set to 1.0e-08:
x=256.1944566599, dx=1.9689009523
order=10, steps=362
 
Default step control with absolute and relative tolerances set to 1.0e-08:
x=256.1921277060, dx=1.9676861175
order=20, steps=156
*/