One-step Taylor method

This method is not recommended in general but it gives an introduction to methods with automatic step control that are described in section Long-time integration.

In order to integrate a system of ODEs one has to

• define an instance of class DMap or LDMap (see Maps and their derivatives ) that describes the vector field, like

  DMap pendulum("time:t;par:omega;var:x,dx;fun:dx,sin(omega*t)-sin(x);");
  pendulum.setParameter("omega",1.);

• define an instance of ODE solver (class DOdeSolver or LDOdeSolver)

  int order = 20;
  double timeStep = 0.125;
  DOdeSolver solver(pendulum,order);
  solver.setStep(timeStep);

Attention

An instance of DOdeSolver can be use to integrate many initial conditions. It is strongly not recommended to create an instance of DOdeSolver for each IVP we want to solve.

• specify the initial condition

  DVector u(2);
  u[0] = 1.; 
  u[1] = 2.;
  double t = 4;

• and then integrate

  DVector y = solver(t,u); 

After the above call

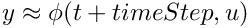• , where 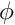is local flow induced by our (nonautonomous) ODE
• value of t is updated to t = t+timeStep

Repeating the last line like

for(int i=0;i<numberOfSteps;++i){
  u = solver(t,u);
  cout << "t=" << t << ", u=" << u << endl;
}  

one can obtain selected points on the trajectory of the point u.

Note

if the system is autonomous one can skip argument t and write

DVector y = solver(u);

Note

Step control is built-in the solver and is turned on by default. In order to obtain a point on the trajectory after user specified time we must turn off step control. This can be achieved by call to

solver.setStep(timeStep);

The above approach does not profit from the automatic step control strategies. There are three additional functions

solver.turnOffStepControl();
solver.turnOnStepControl();
solver.onOffStepControl(booleanArgument);

that manage step control. See Error tolerance and step control for more details on step control strategies and parameters.

Complete example (from examples/odes/DSolverExample.cpp):

#include <cstdio>
#include "capd/capdlib.h"
 
using namespace capd;
 
int main(){
  // define an instance of class DMap that describes the vector field
  DMap pendulum("time:t;par:omega;var:x,dx;fun:dx,sin(omega*t)-sin(x);");
  pendulum.setParameter("omega",1.);
 
  // define an instance of ODE solver
  int order = 20;
  DOdeSolver solver(pendulum,order);
 
  // We set a fixed time step - this disables automatic step control.
  // If one really wants to use fixed time step, it is recommended to put a floating point number with many tailing zeros in the mantissa.
  solver.setStep(0.125);
 
  // specify initial condition
  DVector u(2);
  u[0] = 1.;
  u[1] = 2.;
  double t = 4;
 
  // use one step Taylor method to integrate
  do{
    u = solver(t,u);
    printf("t=%6f, x=%6f, dx=%6f\n",t,u[0],u[1]);
  }while(t<5);
 
  return 0;
}
 
/* output:
t=4.125000, x=1.236999, dx=1.788258
t=4.250000, x=1.446319, dx=1.558578
t=4.375000, x=1.626223, dx=1.318748
t=4.500000, x=1.775834, dx=1.074735
t=4.625000, x=1.894909, dx=0.830721
t=4.750000, x=1.983628, dx=0.589383
t=4.875000, x=2.042431, dx=0.352264
t=5.000000, x=2.071902, dx=0.120138
*/