Poincare maps - interval-based methods

Poincare map and return time - interval version

Computing rigorous bounds for Poincare map is quite similar to nonrigorous version - see Poincare maps - nonrigorous methods. We have to specify initial condition as doubleton set (see Representation of initial condition)

C0Rect2Set set(...);
// or C0HORect2Set set(...);

and call operator of class IPoincareMap

IPoincareMap pm(solver,section);
interval returnTime; // this time does not need to be initialized because initial time is hidden in the set
IVector Px = pm(set,returnTime);

The following example is a complete proof of the existence of Lyapunov orbit L1 in the Planar Restricted Circular Three Body Problem for a fixed Jacobi constant.

Complete example (from examples/poincare/IPoincareMapExample.cpp):

#include <iostream>
#include "capd/capdlib.h"
using namespace std;
using namespace capd;
using capd::autodiff::Node;
 
/*
* This is vector field of the PCR3BP
* @param in is an array of independent variables
* @param out is an array of dependent variables, i.e. out = f(in)
* @param params - parameters of the map. Here we assume that mu=params[0] is a relative mass of Jupiter
*/
void pcr3bpVectorField(Node /*t*/, Node in[], int /*dimIn*/, Node out[], int /*dimOut*/, Node params[], int /*noParams*/)
{
  // Try to factorize expression as much as possible.
  // Usually we have to define some intermediate quantities.
  Node mj = 1-params[0]; // relative mass of the Sun
  Node xMu = in[0] + params[0];
  Node xMj = in[0] - mj;
  Node xMuSquare = xMu^2; // square
  Node xMjSquare = xMj^2;
  Node ySquare = in[1]^2;
 
  // power -1.5, for rigorous computation use ONLY REPRESENTABLE CONSTANTS.
  // If exponent is not representable or it is an interval then it should be a parameter of the map.
  Node factor1 = mj*((xMuSquare+ySquare)^-1.5);
  Node factor2 = params[0]*((xMjSquare+ySquare)^-1.5);
  out[0] = in[2];
  out[1] = in[3];
  out[2] = in[0] - xMu*factor1 - xMj*factor2 + 2*in[3];
  out[3] = in[1]*(1 - factor1 - factor2) - 2*in[2];
}
 
// here is a little function that given a symmetric point point on Poincare section y=0
// (x,dx) = (x,0)
// embeds it into energy level, i.e. it computes dy from (x,y=0,dx=0,dy)
interval toEnergyLevel(interval x, interval mu, interval JacobiConstant)
{
  interval mj = 1.-mu;
  return sqrt(sqr(x) + 2.*(mj/abs(x+mu) + mu/abs(x-mj)) + mu*mj - JacobiConstant);
}
 
int main(){
  cout.precision(17);
  int dim=4, noParam=1;
  IMap vf(pcr3bpVectorField,dim,dim,noParam);
  // set value of parameters mu, which is relative mass of Jupiter
  // 0 is index of parameter, 0.0009537 is its new value
  interval mu = 0.0009537;
  vf.setParameter(0, mu);
 
  // define solver, section and Poincare map
  IOdeSolver solver(vf,30);
  ICoordinateSection section(4,1); // the section is y=0, i.e. 1 coordinate of 4
  IPoincareMap pm(solver,section);
 
  // The following set lies on Poincare section y=0 and is invariant under reversing symmetry of the system.
  // It contains L1 Lyapunov orbit for Oterma's energy value C=3.03.
  interval JacobiConstant = 3.03;
  IVector L1(4);
  L1[0] = 0.9208034913207435 + interval(-1,1)*5e-15;
 
  // We will prove that this periodic orbit indeed exist.
  // It is enough to show that there is a point on symmetry line
  // whose trajectory intersects the symmetry line.
  IVector left = leftVector(L1);
  left[3] = toEnergyLevel(left[0],mu,JacobiConstant);
  IVector right = rightVector(L1);
  right[3] = toEnergyLevel(right[0],mu,JacobiConstant);
  L1[3] = toEnergyLevel(L1[0],mu,JacobiConstant);
 
  C0Rect2Set set(L1);
  C0Rect2Set leftSet(left);
  C0Rect2Set rightSet(right);
  left = pm(leftSet);
  right = pm(rightSet);
 
  // compute Poincare map and print output
  cout << "P(left)=(" << left[0] << "," << left[2] << ")" << endl;
  cout << "P(right)=(" << right[0] << "," << right[2] << ")" << endl;
 
  // check if the Poincare map is well defined on 'set' and get bound for the return time
  interval returnTime;
  pm(set,returnTime);
  cout << "half return time=" << returnTime << endl;
 
  // check if there is a point that intersect symmetry line
  if(left[2].rightBound()<0. and right[2].leftBound()>0.)
    cout << "The existence of L1 orbit validated with accuracy " << diam(L1[0]) << endl;
  else
    cout << "Could not validate L1 periodic orbit" << endl;
  return 0;
}
/* output:
P(left)=([0.95228712767825907, 0.95228712767837564],[-5.4453340632418458e-13, -3.6066379435840335e-15])
P(right)=([0.9522871276784185, 0.95228712767853274],[3.7447292693664613e-14, 5.685078317048184e-13])
half return time=[1.5410595631933541, 1.5410595631986368]
The existence of L1 orbit validated with accuracy [1.021405182655144e-14, 1.021405182655144e-14]
*/

Derivative of Poincare map.

The class IPoincareMap provides an overloaded operator for computation of Poincare map and its derivative. First, an initial condition for the main equation and for the variational equation must be specified - see Representation of initial condition.

C1Rect2Set set(...);
// or C1HORect2Set set(...);

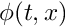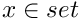We have to define an interval matrix that will store bound for set of monodromy matrices where and 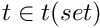is a bound for the return time.

IMatrix monodromyMatrix(...);

Eventually we have to call an operator

IPoincareMap pm(...);
interval returnTime;
IVector P = pm(set,monodromyMatrix,returnTime);

Note

The last argument returnTime is optional and can be skipped for autonomous systems

After successful integration we have

• P bound for the Poincare map at the set of initial conditions set
• bound for the monodromy matrix

Given monodromy matrix we can recompute it to derivative of Poincare map by

IMatrix DP = pm.computeDP(P,monodromyMatrix,returnTime);

Note

for nonautonomous systems the argument returnTime can be skipped

Note

we split computation of derivative of Poincare map into computation of monodromy matrix and solving implicit equation. This is because the user can provide own and optimized routine for recomputation of monodromy matrix to derivative of Poincare map. For user convenience we provide a general routine computeDP.

Note

The matrix DP returned by computeDP is in full dimension. One can take a submatrix of DP that correspond to variables on the section.

Below we give an easy example of computing derivative of Poincare map. See also more advanced examples

• proof of the existence od 3 different periodic orbits for the Rossler system Periodic orbits for the Rossler system
• proof of the existence of 116 periodic orbits for the Lorenz system Multiple periodic solutions for the Lorenz system

Complete example (from examples/poincare/IPoincareMapDerivativeExample.cpp):

#include <iostream>
 
#include "capd/capdlib.h"
 
using namespace capd;
using namespace std;
 
// ----------------------------------- MAIN ----------------------------------------
 
int main()
{
  cout.precision(17);
  try{
    IMap vectorField("par:a,b;var:x,y,z;fun:-(y+z),x+b*y,b+z*(x-a);");
    vectorField.setParameter("a",interval(57)/interval(10));
    vectorField.setParameter("b",interval(2)/interval(10));
 
    IOdeSolver solver(vectorField,20);
 
    // MinusPlus means that the section is crossed with 'x' changing sign from minus to plus
    ICoordinateSection section(3,0); // the section is x=0, i.e. 0-index coordinate of 3
    IPoincareMap pm(solver,section,poincare::MinusPlus);
 
    // this point is very close to fixed point for the Poincare map
    interval data[] = {0.,-8.3809417428298 , 0.029590060630665};
    IVector u(3, data);
    C1Rect2Set set(u);
    interval returnTime;
    IMatrix monodromyMatrix(3,3);
 
    // compute Poincare map
    IVector P = pm(set,monodromyMatrix,returnTime);
 
    // recompute monodromy matrix to derivative of Poincare map
    IMatrix DP = pm.computeDP(P,monodromyMatrix,returnTime);
 
    // print results
    cout << "   u=" << u << endl;
    cout << "P(u)=" << P << endl;
    cout << "return time = " << returnTime << endl;
    cout << "monodromyMatrix=" << monodromyMatrix << endl;
    cout << "DP(u)=" << DP << endl;
   }catch(exception& e)
  {
    cout << "\n\nException caught: "<< e.what() << endl;
  }
  return 0;
}
 
/* output:
   u={[0, 0],[-8.3809417428297994, -8.3809417428297994],[0.029590060630665001, 0.029590060630665001]}
P(u)={[-7.3856090901169207e-13, 7.3856090901169561e-13],[-8.3809417428304709, -8.380941742829652],[0.029590060630664217, 0.029590060630669816]}
return time = [5.8810884555538525, 5.8810884555539493]
monodromyMatrix={
{[0.50685970275883696, 0.50685970276038284],[-2.4490247655247228, -2.4490247655218584],[0.42637843295482369, 0.42637843295635924]},
{[-0.59178625525463191, -0.59178625525322748],[-1.9133051621553399, -1.9133051621525994],[1.881725117656958, 1.881725117658358]},
{[0.0016796765683386335, 0.0016796765683475363],[-0.010279868615699331, -0.010279868615671371],[0.00249192754290111, 0.002491927542910677]}
}
DP(u)={
{[-1.596056620201125e-12, 1.596056620201125e-12],[-3.1072922013208881e-12, 3.1068481121110381e-12],[-1.57773794029481e-12, 1.5777934514460412e-12]},
{[-0.49005513908904019, -0.49005513908721571],[-2.4048455658571841, -2.4048455658533383],[1.9673029484794418, 1.9673029484812423]},
{[-0.00022220565884599518, -0.00022220565882650795],[-0.0010904289145296838, -0.00109042891446786],[0.00089203400376549973, 0.00089203400378485296]}
}
*/