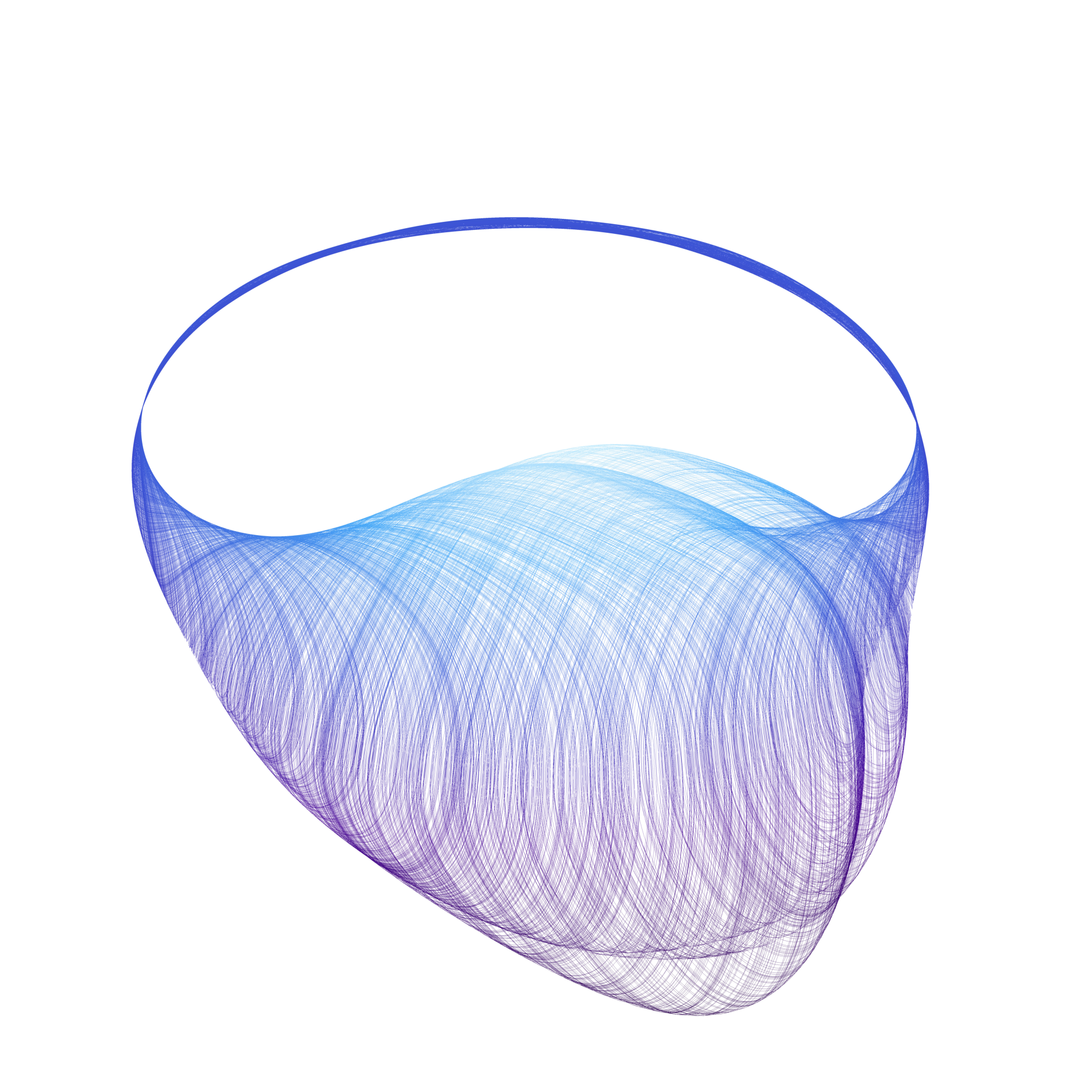
The CAPD library has been used in several articles in which chaotic dynamics, bifurcations, heteroclinic/homoclinic solutions and periodic orbits were studied.
- The existence of simple choreographies for the n-body problem
- Homoclinic and heteroclinic solutions
- Chaotic dynamics for various ODE's
- Invariant curves through the KAM theory
- Cocoon bifurcations
- Rigorous verification of period doubling bifurcations for ODE's
- Rigorous numerics for homoclinic tangencies
- Uniformly hyperbolic attractors for Poincare maps
- Rigorous numerics for dissipative PDE's
- Normally Hyperbolic Invariant Manifolds
- Dynamics of the universal area-preserving map associated with period doubling (written by Tomas Johnson)
|
The existence of simple choreographies
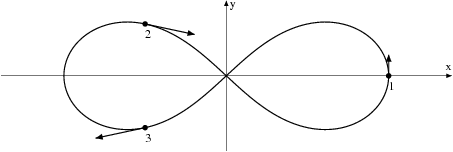
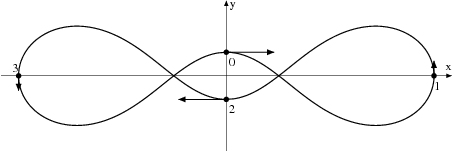
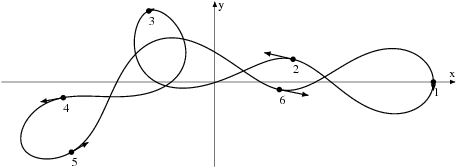
A simple choreography is defined as a collision free solution of the n-body problem in which all the bodies move on the same closed curve with the same time shift. Using validated solvers from the CAPD for ODE's and first order variational equations we were able to prove the existence of some choreographies for various numbers of bodies. Also the linear stability of the well known figure eight choreography was verified. References:
|
|
All the choreographies presented below are proved to exist.
|