The CAPD library has been used in several articles in which chaotic dynamics, bifurcations, heteroclinic/homoclinic solutions and periodic orbits were studied.
- The existence of simple choreographies for the n-body problem
- Homoclinic and heteroclinic solutions
- Chaotic dynamics for various ODE's
- Invariant curves through the KAM theory
- Cocoon bifurcations
- Rigorous verification of period doubling bifurcations for ODE's
- Rigorous numerics for homoclinic tangencies
- Uniformly hyperbolic attractors for Poincare maps
- Rigorous numerics for dissipative PDE's
- Normally Hyperbolic Invariant Manifolds
- Dynamics of the universal area-preserving map associated with period doubling (written by Tomas Johnson)
|
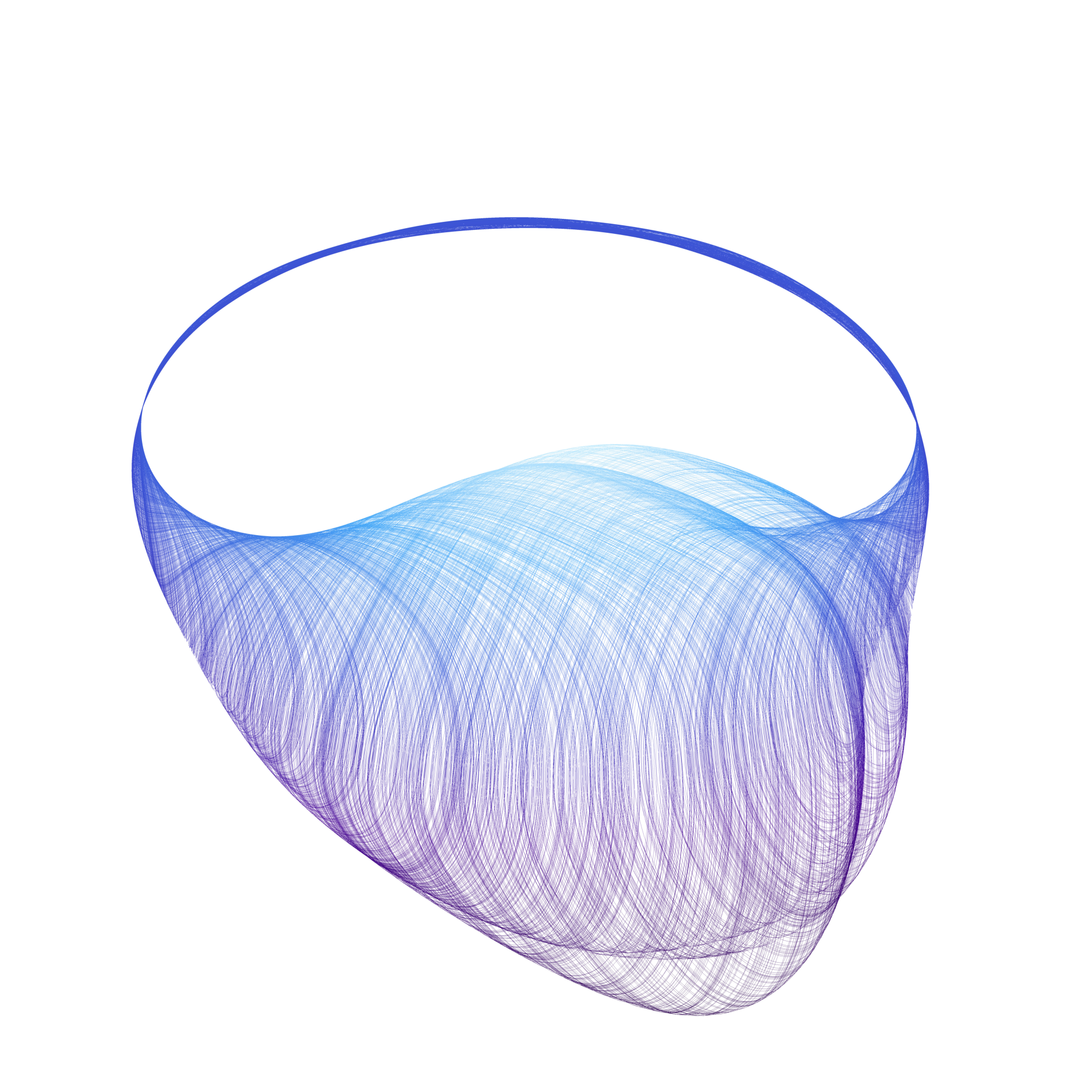
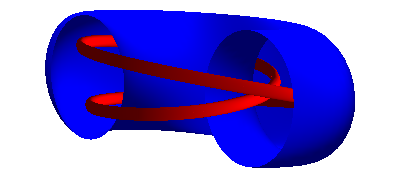
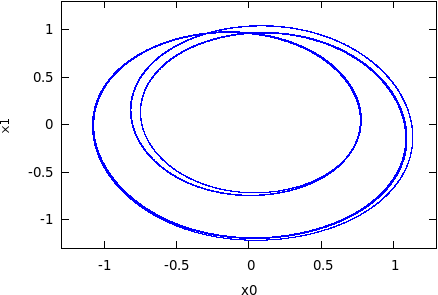
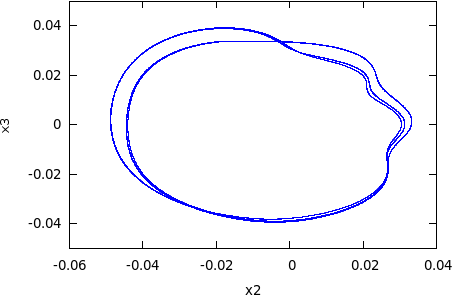
Uniformly hyperbolic attractors for Poincare maps.
Hyperbolic systems contracting volume often manifest robust attractors. There are well known model maps that admits hyperbolic attractor, like Smale map or Plykin map on the sphere. It general, it is rather difficult to prove analytically that a given map or an ODE possesses a hyperbolic chaotic invariant set. We proposed an algorithm for computer assisted verification if a map possesses uniformly hyperbolic invariant set. As a test case we applied the algorithm to the model Smale map S(x,y,t) = (0.1x+0.5cos(t),0.1y+0.5sin(t),2t) where (x,y,t)∊ D2⨯𝓢1 to prove the existence of an uniformly hyperbolic attractor. The other example we considered is the well known Henon map Ha,b(x,y) = (a - x2 + by, x) The hyperbolicity of this map for various parameter values has been studied by many authors, also by means of computer assisted approach (for example, Hruska, Arai, Mazur and Tabor). Our aim was to see if the proposed method works in this relatively easy example. The main motivation for developing new algorithms was to prove the Kuznetsov conjecture. In 2005 he proposed a non-autonomous system that apparently possesses hyperbolic attractor of the Smale-Williams type in the Poincare map. The system is given by
x' = ω u
Theorem. Consider the above system with the parameter values ω=2π, A=5, T=6, ε=0.5.
Let P : ℝ4→ℝ4 be a Poincare map defined as a time T shift along the trajectories.
The set B and an animation of the toroidal attracting domain is shown below. Reference:
|
|
|