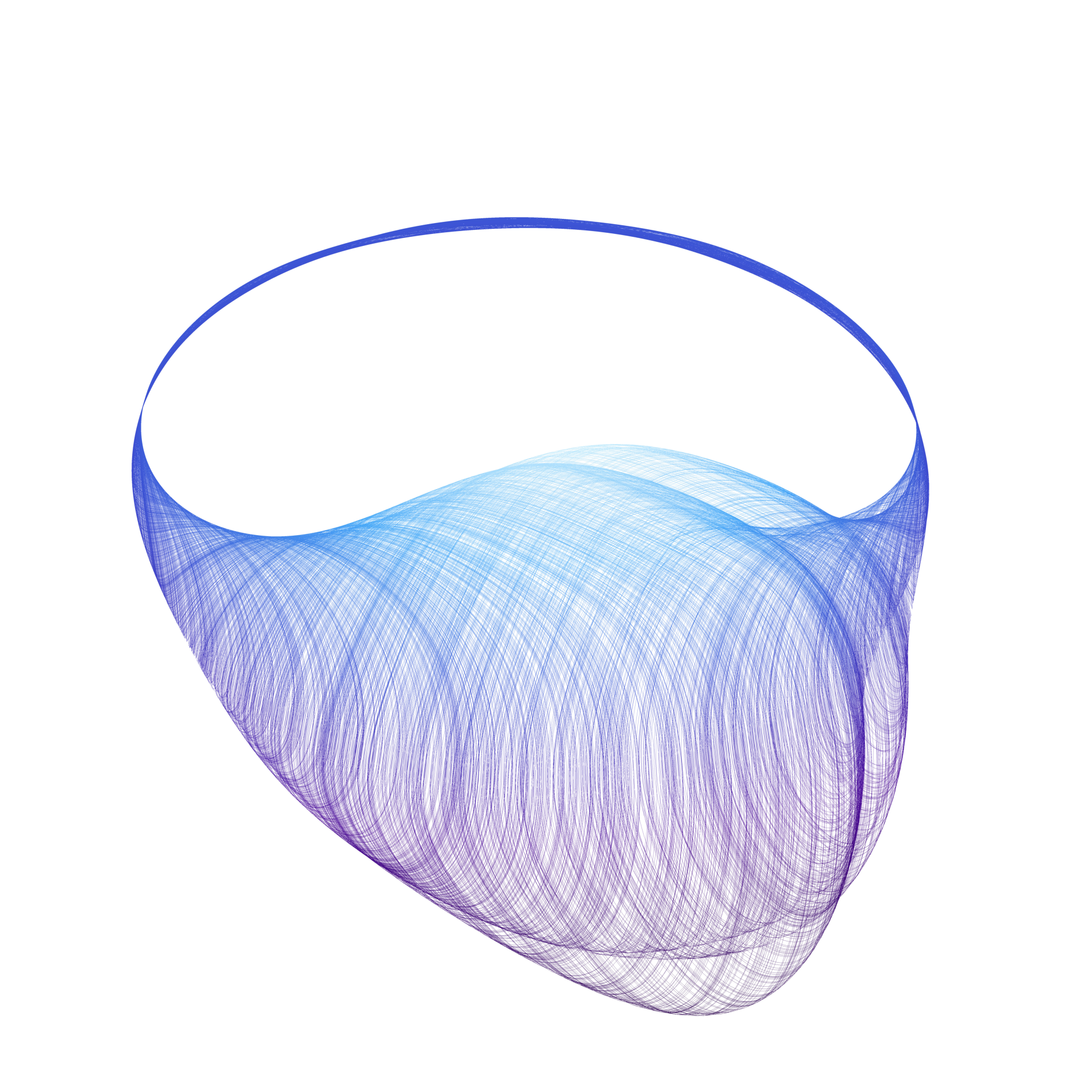
The CAPD library has been used in several articles in which chaotic dynamics, bifurcations, heteroclinic/homoclinic solutions and periodic orbits were studied.
- The existence of simple choreographies for the n-body problem
- Homoclinic and heteroclinic solutions
- Chaotic dynamics for various ODE's
- Invariant curves through the KAM theory
- Cocoon bifurcations
- Rigorous verification of period doubling bifurcations for ODE's
- Rigorous numerics for homoclinic tangencies
- Uniformly hyperbolic attractors for Poincare maps
- Rigorous numerics for dissipative PDE's
- Normally Hyperbolic Invariant Manifolds
- Dynamics of the universal area-preserving map associated with period doubling (written by Tomas Johnson)
|
Homoclinic and heteroclinic solutions
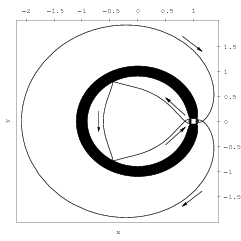
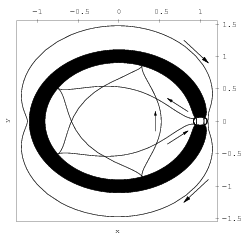
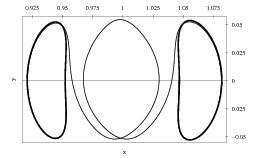
Homoclinic and heteroclinic connections of hyperbolic objects play an important role in the study of dynamical systems from a global point of view. They were used in the design of space missions using libration point dynamics, among which the Genesis has been the first one to make use of a heteroclinic connection. For the design of such missions, the circular Restricted Three Body Problem (RTBP) is the natural problem to start with. Of special interest are the L1 and L2 libration points because of their suitability to place stationary satellites. In [1] we proposed a method for rigorous verification of the existence of homoclinic and heteroclinic points for planar maps. The method has been applied to the Henon map [1] and to the Planar Restricted Three Body Problem [2,3]. Using validated solvers from the CAPD for ODE's and first order variational equations we were able to prove the existence of symbolic dynamics, homoclinic and heteroclinic solutions between Lyapunov periodic orbits for parameter values corresponding to the Oterma comet in the Sun-Jupiter system. Later [4,5] the method has been generalized to any finite dimensions and successfully applied to the hyperchaotic Rossler system [6] were the proof of the existence of infinitely many of homoclinic and heteroclinic solutions between periodic orbits is given. References:
|
|
Two pairs of verified homoclinic orbits to Lyapunov orbits L1 and L2.
Heteroclinic solution connecting these periodic orbits. The connection in the opposite direction follows from the reversibility of the system.
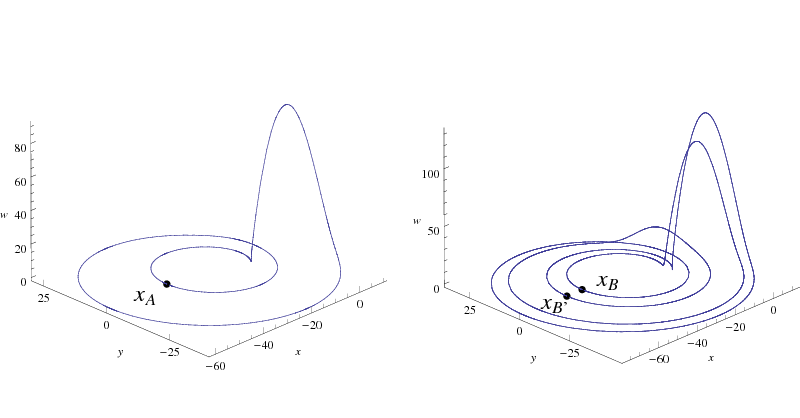
Two periodic solutions for the 4D Rossler system of periods 2 and 4 in the Poincare map. We proved the existence of infinitely many homoclinic and heteroclinic solutions between them. |