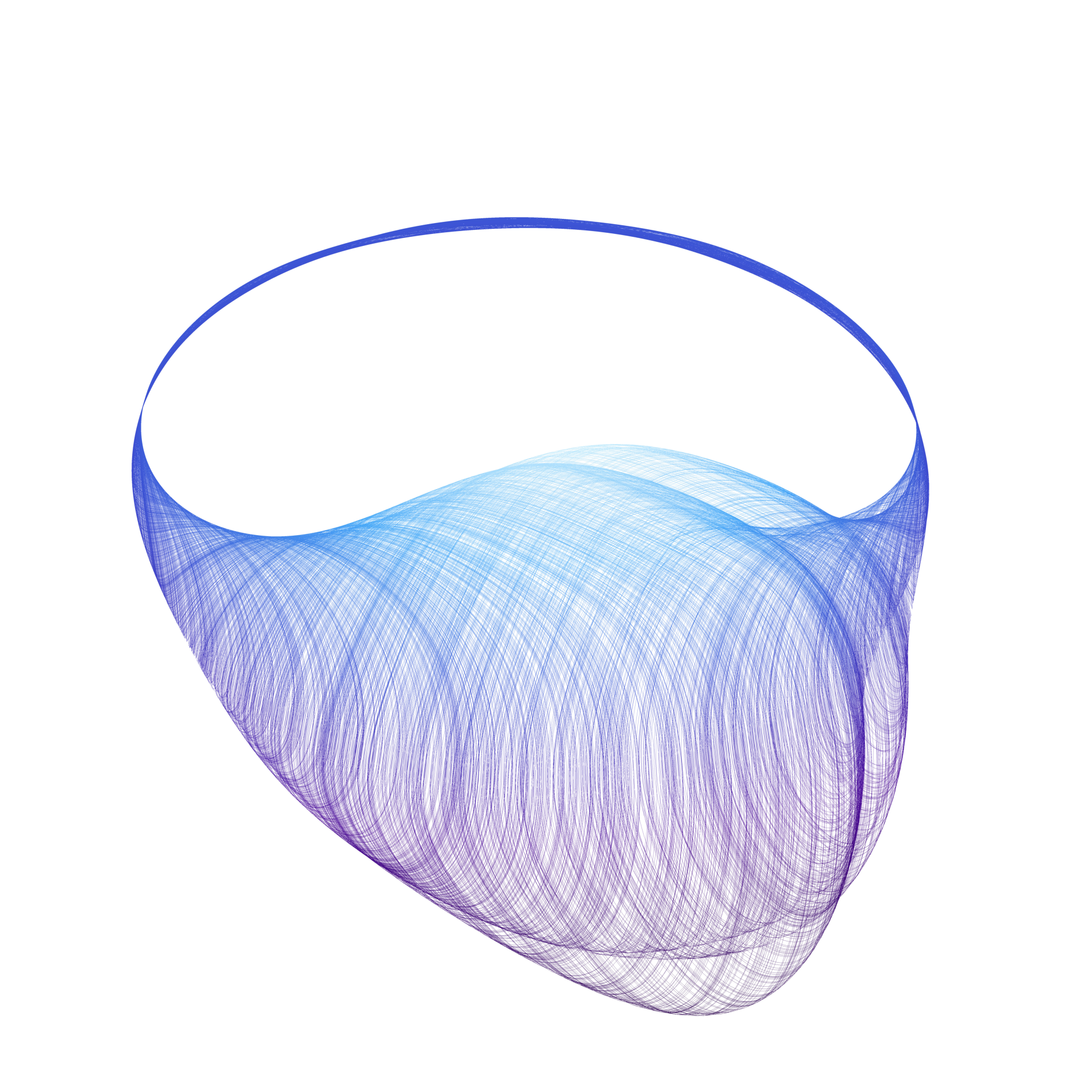
The CAPD library has been used in several articles in which chaotic dynamics, bifurcations, heteroclinic/homoclinic solutions and periodic orbits were studied.
- The existence of simple choreographies for the n-body problem
- Homoclinic and heteroclinic solutions
- Chaotic dynamics for various ODE's
- Invariant curves through the KAM theory
- Cocoon bifurcations
- Rigorous verification of period doubling bifurcations for ODE's
- Rigorous numerics for homoclinic tangencies
- Uniformly hyperbolic attractors for Poincare maps
- Rigorous numerics for dissipative PDE's
- Normally Hyperbolic Invariant Manifolds
- Dynamics of the universal area-preserving map associated with period doubling (written by Tomas Johnson)
|
Normally Hyperbolic Invariant Manifolds
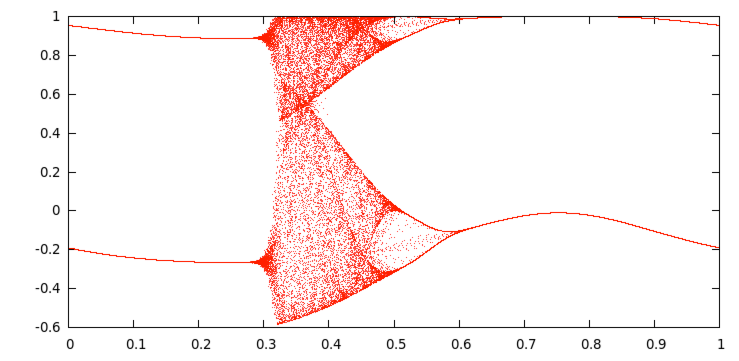
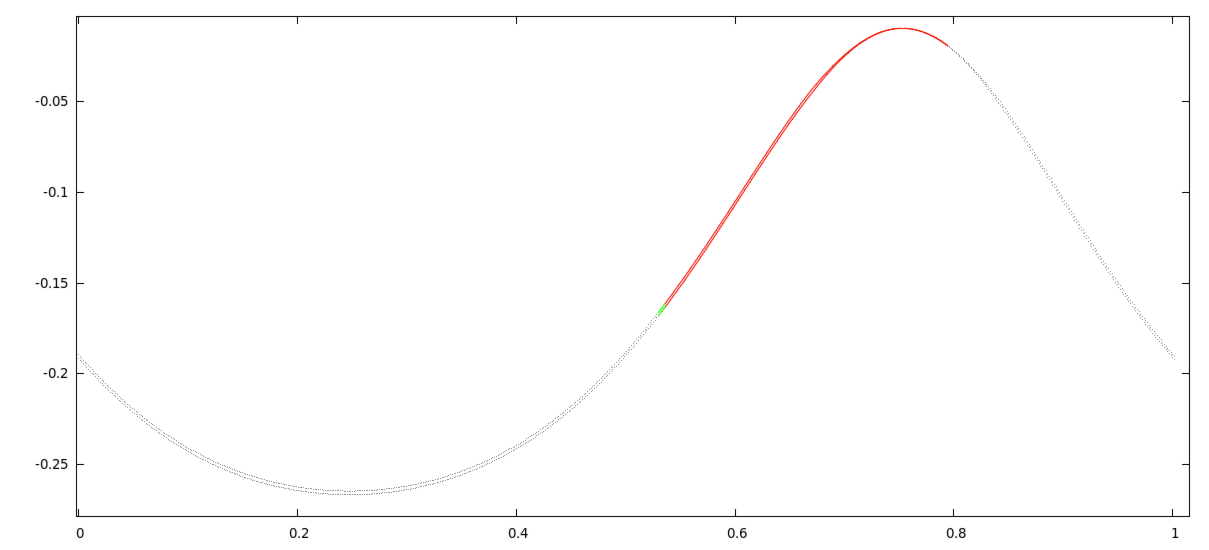
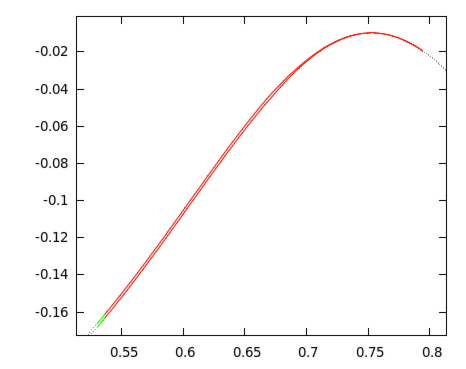
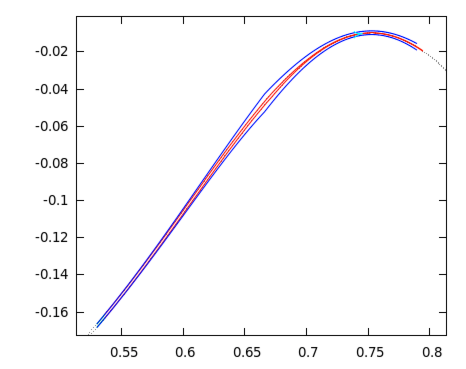
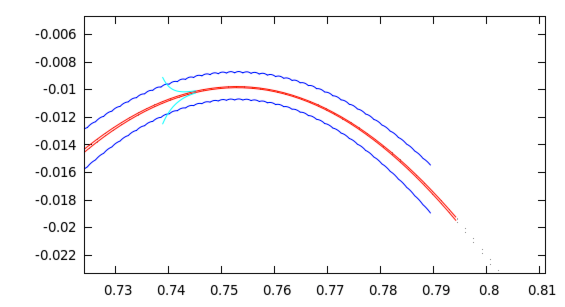
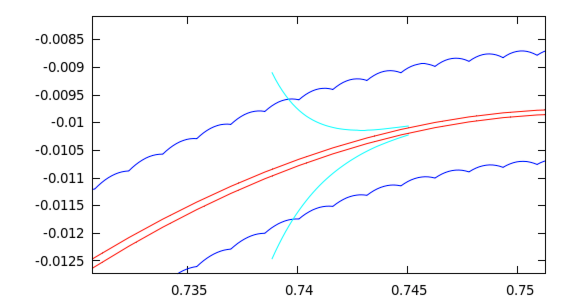
Can one blindly believe numerical simulations? I think that we all know the answer to this. In some cases "numerical evidence" might be very mistakingly interpreted. An example of this is a simple driven logistic map
T : 𝓢1⨯ℝ →𝓢1⨯ℝ, with a=1.31, ε=0.3 and α=g/200, where g is the golden mean g=0.5(√5-1). The map possesses a global attractor, but when standard (double precision) numerical simulation is performed, this attractor seems to be chaotic. This is not the case. When redoing the computations with multiple precision we find that this attractor is in fact composed of two smooth curves. With the CAPD package we have proved that this is the case. The two curves are normally hyperbolic invariant manifolds. In some parts they are strongly contracting, but in many parts they are expanding. Since the map is nasty enough to mislead standard non-rigorous simulations, in our proof we needed to consider multiple precision (tracking 40 digits), combined with 𝓒10 methods. The proof is based on covering relations combined with cone conditions. This description by Maciej Capinski. Reference:
|
|
|