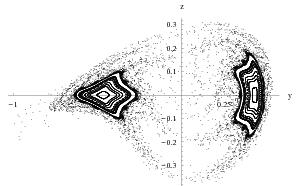
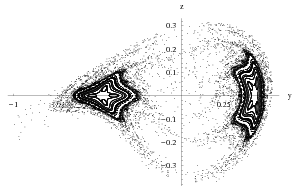
Invariant tori are one of the typical invariant objects which appear in hamiltonian or reversible systems. These objects are of the main interest because they often give rise to so called KAM stability of the solutions. For the case of a planar map, the existence of invariant curves surrounding an elliptic fixed point assures its stability.

Computing of normal forms for hamiltonians is easier than for return maps, since one does not need to integrate the system and its partial derivatives. However, we successfully applied validated C³-C⁵solvers from the CAPD to obtain the proof that for all parameter values ω from the intervals [2, 2.994], [3, 3.997] and [4, 8] a suitable Poincare map for the forced pendulum equations θ'' = -sin(θ) + sin(ωt) possesses invariant curves. In the two gaps in parameters range strong resonances 1:3 and 1:4 appear.

Similar result was obtained for the reversible Michelson system x''' + x' + 0.5x² = c² We have proved that for the parameters c from the intervals [0.05, 0.225] and [0.226, 0.25] there exists an elliptic fixed point for the Poincare map surrounded by invariant curves. Clearly, these curves extend to 2D invariant tori in the full space.

• D. Wilczak, R. Barrio, Systematic Computer-Assisted Proof of branches of stable elliptic periodic orbits and surrounding invariant tori, SIAM Journal on Applied Dynamical Systems, Vol. 16 No. (3), 1618-1649 (2017).
• D. Wilczak, P. Zgliczyński, C^r-Lohner algorithm, Schedae Informaticae, Vol. 20, 9-46 (2011).

Invariant curves in the Poincare section for the Michelson system before and after strong 1:4 resonance. Parameter values are c=0.225 and c=0.226, respectively

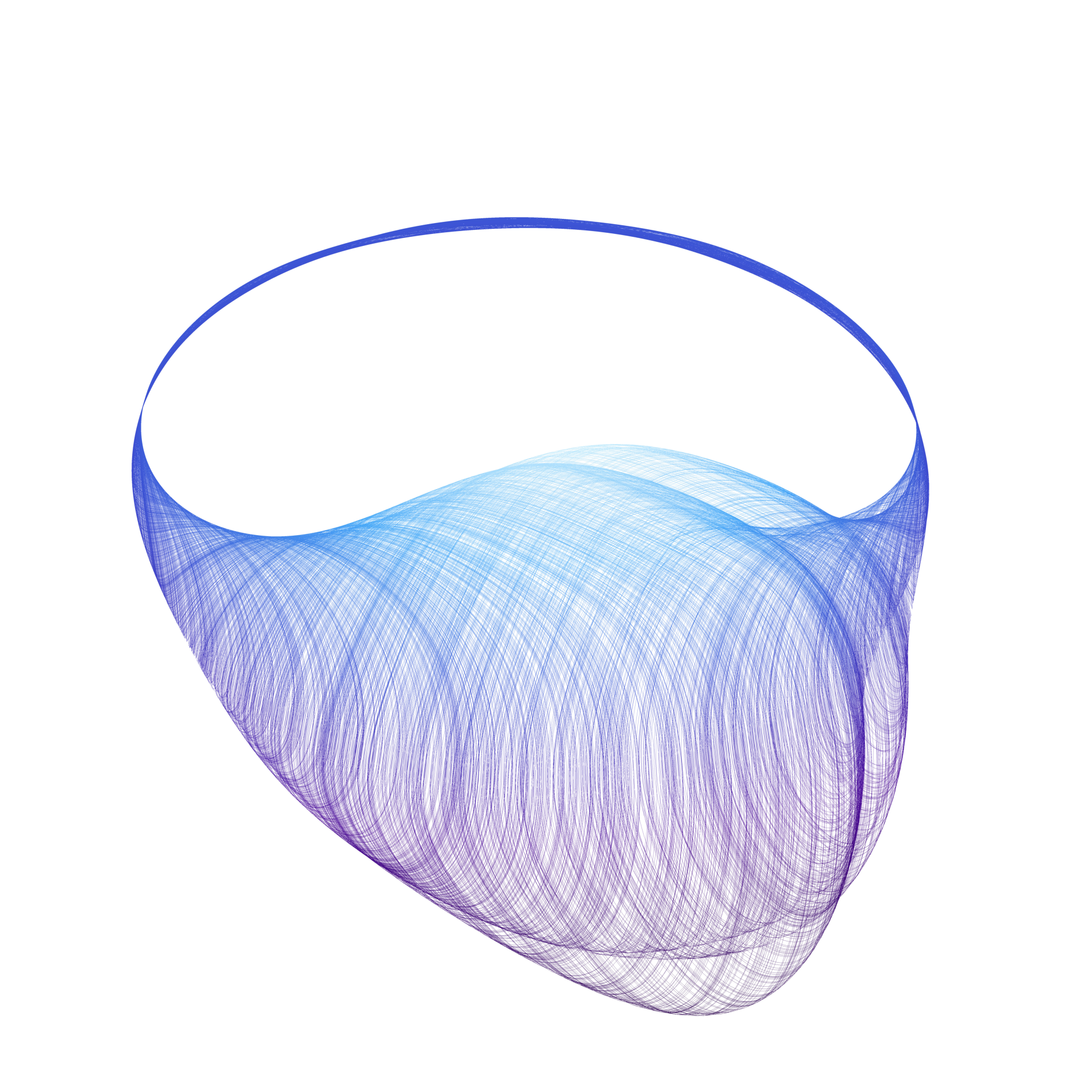
Phase portrait of the Poincare map when the parameter varies.