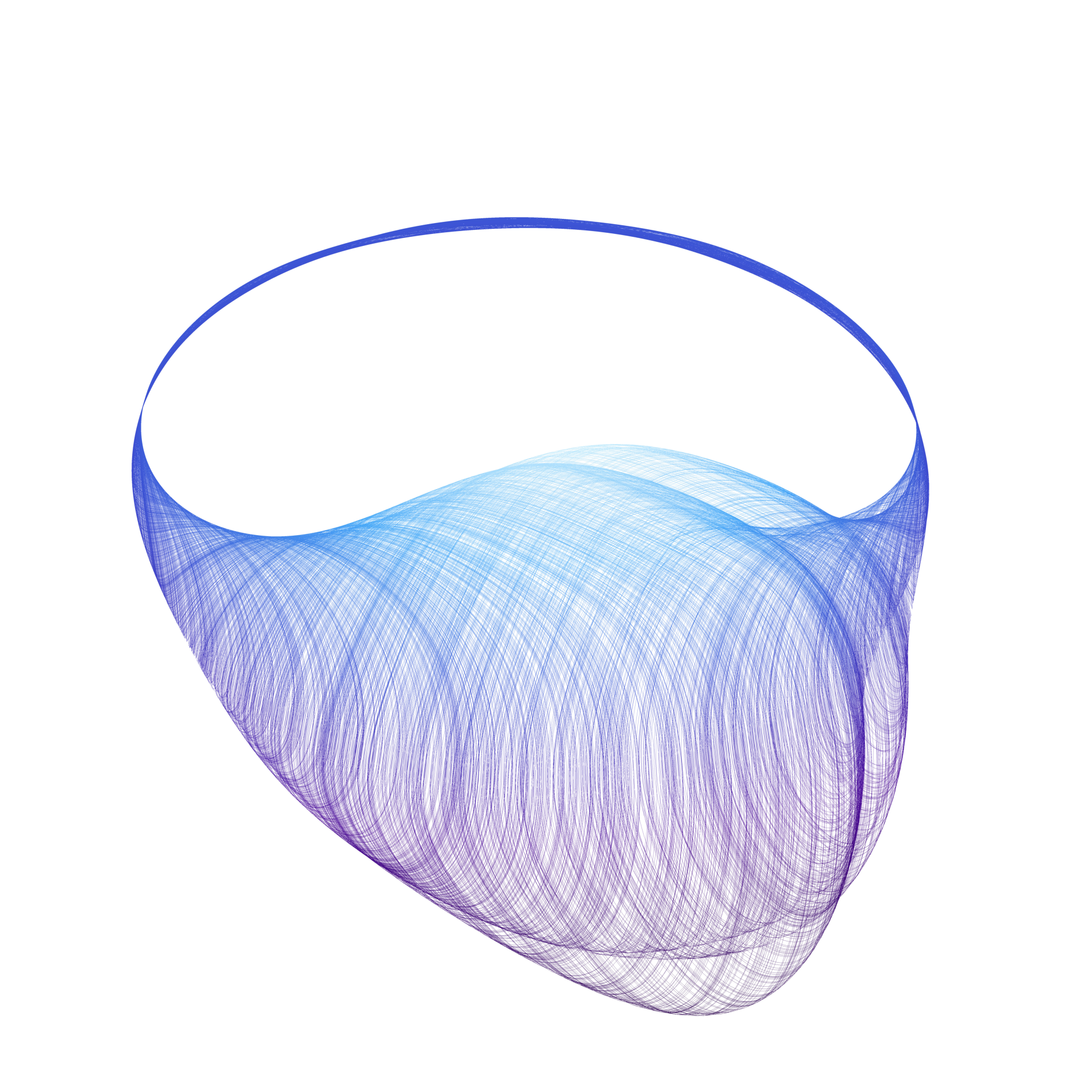
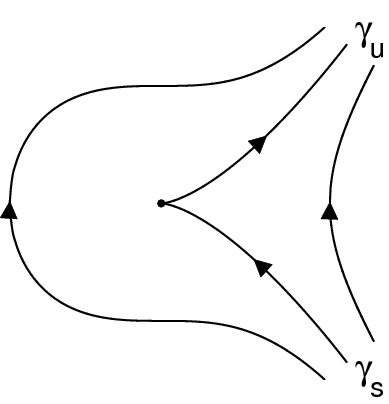
Cocoon bifurcation is a global phenomenon which occurs in 3D reversible ODE's. It has been shown [1] that under some nondegeneracy condition such a vector fields possesses a cascade of heteroclinic tangencies accumulating to new born saddle-node periodic solution. Because of the shape of unstable and stable manifolds of the equilibria these cascades are called cocooning bifurcations.

In [2] we have proved that such a cascade of cocoon bifurcations occurs in the Michelson system x''' + x' + 0.5x² = c² where the periodic orbit to which tangencies accumulate is for some parameter value from the interval [1.2662323370670545, 1.2662323370713253].

The proof required rigorous enclosure for the first and second order derivatives of the Poincare map. Here we used C¹-C²solvers from the CAPD to obtain rigorous bounds for these derivatives.

1. F. Dumortier, S. Ibanez, H. Kokubu, Cocoon bifurcation in three dimensional reversible vector fields, Nonlinearity 19 (2006), 305-328.
2. H. Kokubu, D. Wilczak, P. Zgliczyński, Rigorous verification of cocoon bifurcations in the Michelson system, Nonlinearity 20, No.9, 2147-2174 (2007).

The proof required rigorous estimation of the unstable set of the nonhyperbolic periodic orbit in an explicit neighbourhood of this orbit.

The existence of transversal intersection of the unstable set with 2D stable manifold of a hyperbolic equilibrium results in the existence of cocoon bifurcations.