The CAPD library has been used in several articles in which chaotic dynamics, bifurcations, heteroclinic/homoclinic solutions and periodic orbits were studied.
- The existence of simple choreographies for the n-body problem
- Homoclinic and heteroclinic solutions
- Chaotic dynamics for various ODE's
- Invariant curves through the KAM theory
- Cocoon bifurcations
- Rigorous verification of period doubling bifurcations for ODE's
- Rigorous numerics for homoclinic tangencies
- Uniformly hyperbolic attractors for Poincare maps
- Rigorous numerics for dissipative PDE's
- Normally Hyperbolic Invariant Manifolds
- Dynamics of the universal area-preserving map associated with period doubling (written by Tomas Johnson)
|
Rigorous verification of period doubling bifurcations for ODE's
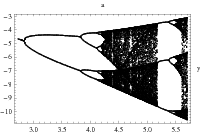
The period doubling is well known scenario for the onset of chaos. It has been studied and understand better through the renormalization theory. The existence of an universal area-preserving map associated to period doubling has been proved. Our goal was to verify a part of bifurcation diagram of periodic orbits of ODE's. We proposed a geometric method for verification of the existence of a single period doubling for a map. Also a full description of the maximal invariant set in a neighbourhood of period doubling is given. The method assumes, that we can compute all derivatives of the map up to the third order. Using validated C1-C3solvers from the CAPD we verified a part of bifurcation diagram for a Poincare map of the Rossler system x' = -y-z, y' = x+by, z' = b+z(x-a) for the parameter b=0.2 and with a∊[2.83244,3.837358168411]. The existence of two period doublings (1→2→4) and of a branch of period two points connecting them has been proved. Reference:
|
|
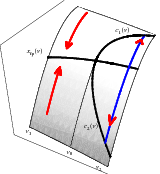
(Left) Observed bifurcation diagram of periodic orbits for the Rossler system with b=0.2 (Right) The dynamics on the center manifold in a neighbourhood of bifurcation point. Before bifurcation the maximal invariant set in a neighbourhood of PD is just a point. After bifurcation the maximal invariant set consists of fixed point, period two points and intersection of their stable/unstable manifolds (in blue).
|